Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có 2 cách để tính khoảng cách giữa hai đường thẳng chéo nhau



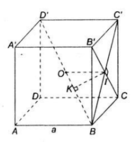
a) Ta có:
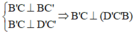
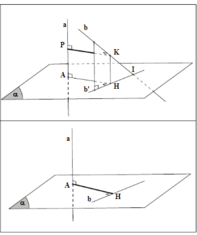
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
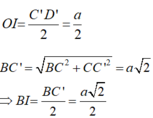
Vì ΔIOB vuông tại I có đường cao IK nên:
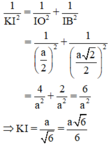

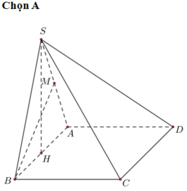
Do \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;SC\right)=d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Trong tam giác SAD, kẻ \(AH\perp SD\) \(\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
Tam giác SAD vuông cân tại A \(\Rightarrow AH=\dfrac{AD}{\sqrt{2}}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow d\left(SC;AB\right)=\dfrac{a\sqrt{2}}{2}\)

Theo nhận xét trang 117
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại
Áp dụng chứng minh câu 3 trang 116, ta có đpcm
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Áp dụng chứng minh câu 4 trang 116, ta có đpcm

Chọn B.
Lời giải.
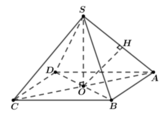
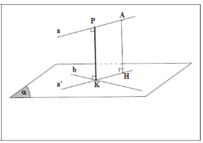
Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD ⇒ S O ⊥ ( A B C D ) . Qua O kẻ đường thẳng OH vuông góc với SA với H ∈ SA
Ta có
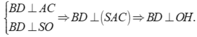
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
![]()
Tam giác SAO vuông tại O, có đường cao OH suy ra
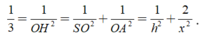
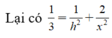
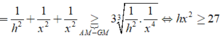
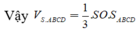
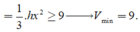

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.