Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0

Bài 4:
=>(x-5)*3/10=1/5x+5
=>3/10x-3/2=1/5x+5
=>1/10x=5+3/2=6,5
=>0,1x=6,5
=>x=65

a) Ta có : \(A=\dfrac{x^2+y^2+5}{x^2+y^2+3}=1+\dfrac{2}{x^2+y^2+3}\)
Dễ thấy \(x^2\ge0;y^2\ge0\forall x;y\)
nên \(x^2+y^2+3\ge3\)
\(\Leftrightarrow\dfrac{1}{x^2+y^2+3}\le\dfrac{1}{3}\)
<=> \(\dfrac{2}{x^2+y^2+3}\le\dfrac{2}{3}\)
\(\Leftrightarrow A=1+\dfrac{2}{x^2+y^2+3}\le\dfrac{5}{3}\)
\(\Rightarrow A_{max}=\dfrac{5}{3}\)(Dấu "=" xảy ra khi x = y = 0)

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 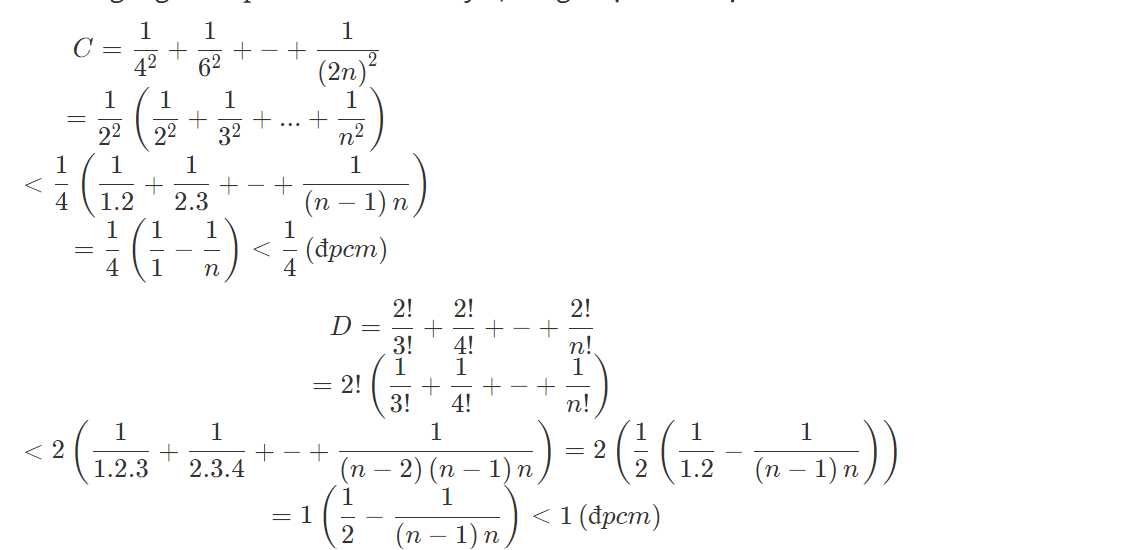

=>-3<n<=4
hay \(n\in\left\{-2;-1;0;1;2;3;4\right\}\)