Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 +
+  +
+  ≥ 3.
≥ 3.
Đặt b + c – a = x > 0 (1); a + c – b = y > 0 (2); a + b – c = z > 0 (3)
Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c = 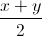
Tương tự a = 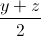 ; b =
; b = 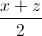
Do đó  +
+  +
+  =
= 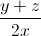 +
+ 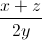 +
+ 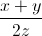 =
=  (
(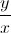 +
+ 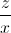 +
+  +
+  +
+ 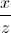 +
+  )
)
=  [(
[(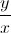 +
+  ) + (
) + (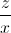 +
+ 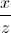 ) + (
) + ( +
+  )] ≥
)] ≥  (2 + 2 + 2) = 3.
(2 + 2 + 2) = 3.
Vậy  +
+  +
+  ≥ 3.
≥ 3.

\(\dfrac{1}{a+b-c}+\dfrac{1}{b+c-a}\ge\dfrac{4}{a+b-c+b+c-a}=\dfrac{2}{b}\)
Tương tự:
\(\dfrac{1}{a+b-c}+\dfrac{1}{c+a-b}\ge\dfrac{2}{a}\) ; \(\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\ge\dfrac{2}{c}\)
Cộng vế:
\(2\left(\dfrac{1}{a+b-c}+\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\right)\ge\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}\)
\(\Rightarrow\dfrac{1}{a+b-c}+\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
cho em hỏi tại sao 1/a+b-c +1/b+c-a>=4/a+b-c+b+c-a vậy ạ

-Đặt \(\left\{{}\begin{matrix}b+c-a=x>0\\c+a-b=y>0\\a+b-c=z>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2c=x+y\\2a=y+z\\2b=z+x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}c=\dfrac{x+y}{2}\\a=\dfrac{y+z}{2}\\b=\dfrac{z+x}{2}\end{matrix}\right.\)
\(A=\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}=\dfrac{\dfrac{y+z}{2}}{x}+\dfrac{\dfrac{z+x}{2}}{y}+\dfrac{\dfrac{x+y}{2}}{z}=\dfrac{1}{2}\left(\dfrac{y+z}{x}+\dfrac{z+x}{y}+\dfrac{x+y}{z}\right)=\dfrac{1}{2}\left[\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)+\left(\dfrac{x}{z}+\dfrac{z}{x}\right)\right]\ge\dfrac{1}{2}.\left(2+2+2\right)=3\left(đpcm\right)\)
-Dấu "=" xảy ra khi \(a=b=c\)

Xét tam giác ABC có ba cạnh BC = a, CA = b, AB = c. Phân giác của các góc A, B, C lần lượt là AD = x, BE = y, CF = z.
Kẻ DM // AB \((M\in AC)\).
Ta có \(\widehat{ADM}=\widehat{BAD}=\widehat{MAD}\Rightarrow\) Tam giác AMD cân tại M.
Do đó AM = MD.
Áp dụng định lý Thales với DM // AB ta có:
\(\dfrac{MD}{AB}=\dfrac{CM}{AC}=1-\dfrac{AM}{AC}=1-\dfrac{DM}{AC}\Rightarrow\dfrac{MD}{AB}+\dfrac{MD}{AC}=1\Rightarrow\dfrac{1}{MD}=\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{b}+\dfrac{1}{c}\).
Mặt khác theo bất đẳng thức tam giác ta có \(x=AD< AM+MD=2MD\Rightarrow MD>\dfrac{x}{2}\Rightarrow\dfrac{1}{MD}< \dfrac{2}{x}\Rightarrow\dfrac{1}{b}+\dfrac{1}{c}< \dfrac{2}{x}\).
Tương tự \(\dfrac{1}{c}+\dfrac{1}{a}< \dfrac{2}{y};\dfrac{1}{a}+\dfrac{1}{b}< \dfrac{2}{z}\).
Cộng vế với vế của các bđt trên rồi rút gọn ta có đpcm.

Câu hỏi của Phạm Thị Hường - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài làm ở link này nhé!

`1/a^2+1/b^2+1/c^2<=(a+b+c)/(abc)`
`<=>1/a^2+1/b^2+1/c^2<=1/(ab)+1/(bc)+1/(ca)`
`<=>2/a^2+2/b^2+2/c^2<=2/(ab)+2/(bc)+2/(ca)`
`<=>1/a^2-2/(ab)+1/b^2+1/b^2-2/(bc)+1/c^2+1/c^2-2/(ac)+1/a^2<=0`
`<=>(1/a-1/b)^2+(1/b-1/c)^2+(1/c-1/a)^2<=0`
Mà `(1/a-1/b)^2+(1/b-1/c)^2+(1/c-1/a)^2>=0`
`=>(1/a-1/b)^2+(1/b-1/c)^2+(1/c-1/a)^2=0`
`<=>1/a=1/b=1/c`
`<=>a=b=c`
`=>` tam giác này là tam giác đều
`=>hata=hatb=hatc=60^o`
Áp dụng bđt cosi với hai số dương:
\(\dfrac{1}{a^2}+\dfrac{1}{b^2}\ge\dfrac{2}{ab}\) ; \(\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge\dfrac{2}{bc}\) ; \(\dfrac{1}{a^2}+\dfrac{1}{c^2}\ge\dfrac{2}{ac}\)
\(\Rightarrow2\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\ge2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}\right)\)
\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}\) (*)
Theo giả thiết có: \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\le\dfrac{1}{bc}+\dfrac{1}{ac}+\dfrac{1}{ab}\) (2*)
Từ (*), (2*) ,dấu = xảy ra \(\Leftrightarrow a=b=c\)
=> Tam giác chứa ba cạnh a,b,c thỏa mãn gt là tam giác đều
=> Số đo các góc là 60 độ

a)a,b,c là độ dài 3 cạnh của 1 tam giác
\(\Rightarrow a< b+c\Rightarrow a^2< ab+ac\)
TT\(\Rightarrow b^2< ba+bc\)
\(c^2< ca+cb\)
Cộng vế theo vế ta có đpcm
b)BĐT\(\Leftrightarrow\dfrac{a}{b+c-a}+\dfrac{1}{2}+\dfrac{b}{a+c-b}+\dfrac{1}{2}+\dfrac{c}{a+b-c}+\dfrac{1}{2}\ge\dfrac{9}{2}\)
\(\Leftrightarrow\dfrac{1}{2}\left(\dfrac{a+b+c}{b+c-a}+\dfrac{a+b+c}{a+c-b}+\dfrac{a+b+c}{a+b-c}\right)\ge\dfrac{9}{2}\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}\right)\ge9\)(đúng theo AM-GM)

Lời giải:
Do $a,b,c>0$ nên:\(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1(1)\)
Vì $a,b,c$ là 3 cạnh tam giác nên theo BĐT tam giác thì:
$a+b>c\Rightarrow 2(a+b)>a+b+c\Rightarrow a+b>\frac{a+b+c}{2}$
$\Rightarrow \frac{c}{a+b}< \frac{2c}{a+b+c}$. Hoàn toàn tương tự với các phân thức còn lại:
\(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}< \frac{2a+2b+2c}{a+b+c}=2(2)\)
Từ $(1);(2)$ ta có đpcm.
câu 1 :Đặt b+c-a=x; a+c-b=y ; a+b-c=z
vì a,b,c là 3 cạnh của tam giác nên
b+c-a>0 ; a+c-b>0 ; a+b-c>0
Đặt biểu thức \(\dfrac{a}{b +c-a}\)+\(\dfrac{b}{c+a-b}\)+\(\dfrac{c}{a+b-c}\)=S thì
2S=\(\dfrac{2a}{b+c-a}\)+\(\dfrac{2b}{c+a-b}\)+\(\dfrac{2c}{a+b-c}\)
mà \(\dfrac{2a}{b+c-a}\)=\(\dfrac{a+c-b+a+b-c}{b+c-a}\)=\(\dfrac{y+z}{x}\) , tương tự
\(\dfrac{2b}{c+a-b}\)=\(\dfrac{x+z}{y}\)
\(\dfrac{2c}{a+b-c}\)=\(\dfrac{x+y}{z}\)
=>2S=\(\dfrac{x+y}{z}\)+\(\dfrac{y+z}{x}\)+\(\dfrac{x+z}{y}\)=\(\dfrac{x}{z}\)+\(\dfrac{y}{z}\)+\(\dfrac{y}{x}\)+\(\dfrac{z}{x}\)+\(\dfrac{x}{y}\)+\(\dfrac{z}{y}\)
ta thấy \(\dfrac{x}{z}\)+\(\dfrac{z}{x}\)=\(\dfrac{x^{2^{ }}+z^2}{xz}\)\(\ge\)\(\dfrac{2xz}{xz}\)=2 tương tự với 2 cặp số nghich đảo còn lại thì ta có 2S\(\ge\)2+2+2=6
nên S\(\ge\)3
dấu = xảy ra \(\Leftrightarrow\)x=y=z
câu 2 :
ta có a+b>c ;b+c>a ; a+c>b
xét \(\dfrac{1}{a+c}\)+\(\dfrac{1}{b+c}\)>\(\dfrac{1}{a+b+c}\)+\(\dfrac{1}{b+c+a}\)=\(\dfrac{2}{a+b+c}\)>\(\dfrac{2}{a+b+a+b}\)=\(\dfrac{1}{a+b}\)
tương tự \(\dfrac{1}{a+b}\)+\(\dfrac{1}{a+c}\)>\(\dfrac{1}{b+c}\);\(\dfrac{1}{a+b}\)+\(\dfrac{1}{b+c}\)>\(\dfrac{1}{a+c}\)
nên điều phải chứng minh
Giúp tớ với các cậu ơi....