Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)

Lời giải:
Sử dụng công thức \(\log_ab=\frac{\ln b}{\ln a}\)
\(\Rightarrow A=\frac{\ln 2}{\ln 3}.\frac{\ln 3}{\ln 4}.\frac{\ln 4}{\ln 5}....\frac{\ln 15}{\ln 16}\)
\(\Leftrightarrow A=\frac{\ln 2}{\ln 16}=\log_{16}2=\frac{1}{4}\)
Đáp án C.

\(D=\frac{\log_2\left(2a^2\right)+\left(\log_2a\right)a^{\log_2\left(\log_2a+1\right)}+\frac{1}{2}\log^2_2a^4}{\log_2a^3\left(3\log_2a+1\right)+1}=\frac{1+2\log_2a+\log_2a\left(\log_2a+1\right)+8\log^2_2a}{3\log_2a.\left(3\log_2a+1\right)+1}\)
\(=\frac{9\log^2_2a+3\log_2a+1}{9\log^2_2a+3\log_2a+1}=1\)

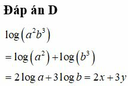
Do a, b, x là những số dương nên ta có:
Ta có: