Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
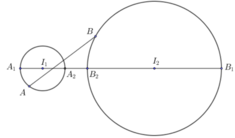
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

Chọn D
Gọi I là trung điểm của AB, suy ra I (1;1;1); ![]()
Phương trình mặt phẳng trung trực của AB: (α): 2x + y -3 = 0.
Vì (2.3 + 1.2 - 3). (2.5 + 1.3 - 3) = 50 > 0 nên B, C nằm về một phía so với (α), suy ra A, C nằm về hai phía so với (α).
Điểm M thỏa mãn MA = MB khi M ∈ (α).
Khi đó MB + MC = MA + MC ≥ AC.
MB + MC nhỏ nhất bằng AC khi M = AC ∩ (α)
Phương trình đường thẳng AC: 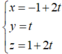
do đó tọa độ điểm M là nghiệm của hệ phương trình
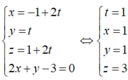
Do đó M (1; 1; 3), a + b + c = 5

Lời giải:
Để hai hàm số cắt nhau tại hai điểm phân biệt thì phương trình
\(\frac{x+1}{x-1}+(2x-m)=0\Leftrightarrow 2x^2-(m+1)x+(m+1)=0\) có hai nghiệm phân biệt
\(\Rightarrow \Delta =(m+1)^2-8(m+1)>0\Leftrightarrow m>7\) hoặc $m<-1$
Hai điểm $A,B$ có hoành độ tương ứng với nghiệm của phương trình giao điểm. Do đó áp dụng hệ thức Viet: \(x_A+x_B=\frac{m+1}{2}\)
Hoành độ trung điểm $AB$ là \(\frac{x_A+x_B}{2}=\frac{m+1}{4}=\frac{5}{2}\Rightarrow m=9\)
Do đó đáp án $C$ là đáp án đúng

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
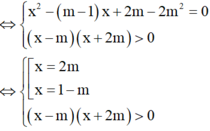
Điều kiện để pt đã cho có 2 nghiệm
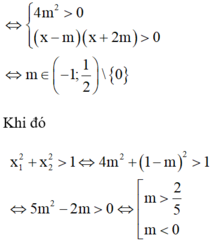
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2
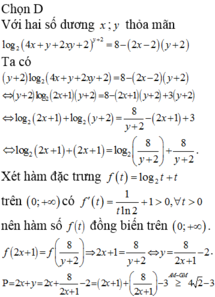
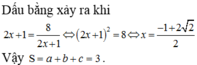

Chọn A