Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

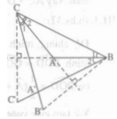
+) Vì AC là đường trung trực của BB'
Suy ra: CB’ =CB ( tính chất đường trung trực)
Do đó,tam giác CBB’ là tam giác cân tại C. Có CA là đường trung trực của BB’ nên đồng thời là đường phân giác nên có ∠C1= ∠C2.
+) Vì AB là đường trung trực của CC' nên BC = BC’.
Suy ra, tam giác BCC’ cân tại B. Lại có BA là đường trung trực nên đồng thời là đường phân giác (tính chất tam giác cân).
Suy ra: ∠B1 = ∠B2 .
+) Ta có: AB, AC lần lượt là đường phân giác của các góc A'BC và góc A'CB; hai đường này cắt nhau tại A.
Vậy ba đường phân giác của tam giác A'BC đồng quy tại A, hay A là điểm nằm trong tam giác A'BC và cách đều ba cạnh của tam giác này.

Vì AC là đường trung trực của BB' nên CB=CB'
=>ΔCBB' cân tại C
hay \(\widehat{BCA}=\widehat{B'CA}\)
Vì AB là đường trung trực của CC' nên BC=BC'
=>ΔBCC' cân tại B
hay \(\widehat{CBA}=\widehat{C'BA}\)
Vì AB và AC lần lượt là các đường phân giác của các góc CBB' và BCB'
và AB cắt AC tại A
nên A là điểm cách đều ba cạnh của ΔA'BC
win-lê chí cường làm ik
Phương- chuẩn bị làm đệ anh đi