TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
CM
5 tháng 8 2017
Đáp án D
Đường thẳng đi qua 2 điểm A và B có vectơ chỉ phương là 
suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
Suy ra phương trình AB: 4( x-3) + 3( y+ 1) = 0 hay 4x+ 3y -9=0
Do M nằm trên Ox nên M( x; 0)
Do d(M; AB)=1 nên
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 10 2019
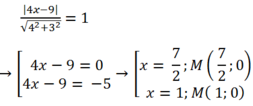
Gọi \(M\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-1-x;4\right)\\\overrightarrow{MB}=\left(1-x;-2\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+2\overrightarrow{MB}=\left(1-3x;0\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|=\sqrt{\left(1-3x\right)^2}\ge0\)
Dấu "=" xảy ra khi \(x=\frac{1}{3}\Rightarrow M\left(\frac{1}{3};0\right)\)
Gọi \(P\left(0;y\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PA}=\left(-1;4-y\right)\\\overrightarrow{PB}=\left(1;-2-y\right)\\\overrightarrow{PC}=\left(3;4-y\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{PA}+2\overrightarrow{PB}-4\overrightarrow{PC}=\left(-11;5y-16\right)\)
\(\Rightarrow\left|\overrightarrow{PA}+\overrightarrow{PB}-4\overrightarrow{PC}\right|=\sqrt{11^2+\left(5y-16\right)^2}\ge11\)
Dấu "=" xảy ra khi \(5y-16=0\Rightarrow y=\frac{16}{5}\Rightarrow P\left(0;\frac{16}{5}\right)\)
Gọi \(M\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(a-2;3\right)\\\overrightarrow{BM}=\left(a-1;-4\right)\end{matrix}\right.\)
\(\Rightarrow\frac{a-2}{a-1}=\frac{3}{-4}\Rightarrow a=\frac{11}{7}\Rightarrow M\left(\frac{11}{7};0\right)\)