NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
1
VT
0
7 tháng 3 2021
A=1/2+1/3+..+1/2019 < 1>
A= 1+1/2+1/3+..+1/2019 < 1>
A=1+1/2+1/3+..+1/2019 <1>
A=1+1/2+1/3+..+1/2019 <2018>
Vì 2018/2019 <1>
nên A=1/2+1/3+..+1/2019<1>
=> A=1/2+1/3+..+1/2019 không phải là số tự nhiên.
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Mình chưa hiểu cách bạn làm với dấu <1> cho lắm.
Theo mình hiểu thì bạn đang chứng minh $A< 1$ nên $A$ không phải số tự nhiên. Mà điều này thì sai vì $A=1+(\frac{1}{2}+\frac{1}{3}+...)$ hiển nhiên lớn hơn $1$.
TT
1
NH
0
DL
18 tháng 7 2017
a) Giả sử 3 số đó là a,a+1,a+2
Tổng của chúng : a + a + 1 + a + 2 = 3a + 3 chia hết cho 3 (đpcm)
C2: Nếu a chia hết cho 3 thì a có dạng 3k và a +1 = 3k + 1
a + 2 =3k+2
a + a + 1 + a + 2 = 3k + 3k+ 1 +3k+2 cũng tương tự với trường hợp a : 3 dư 1 và dư 2
b) Gọi 4 số đó là a,a+1,a+2,a+3
a + a + 1 + a + 2 + a + 3 = 4a + 6 không chia hết cho 4
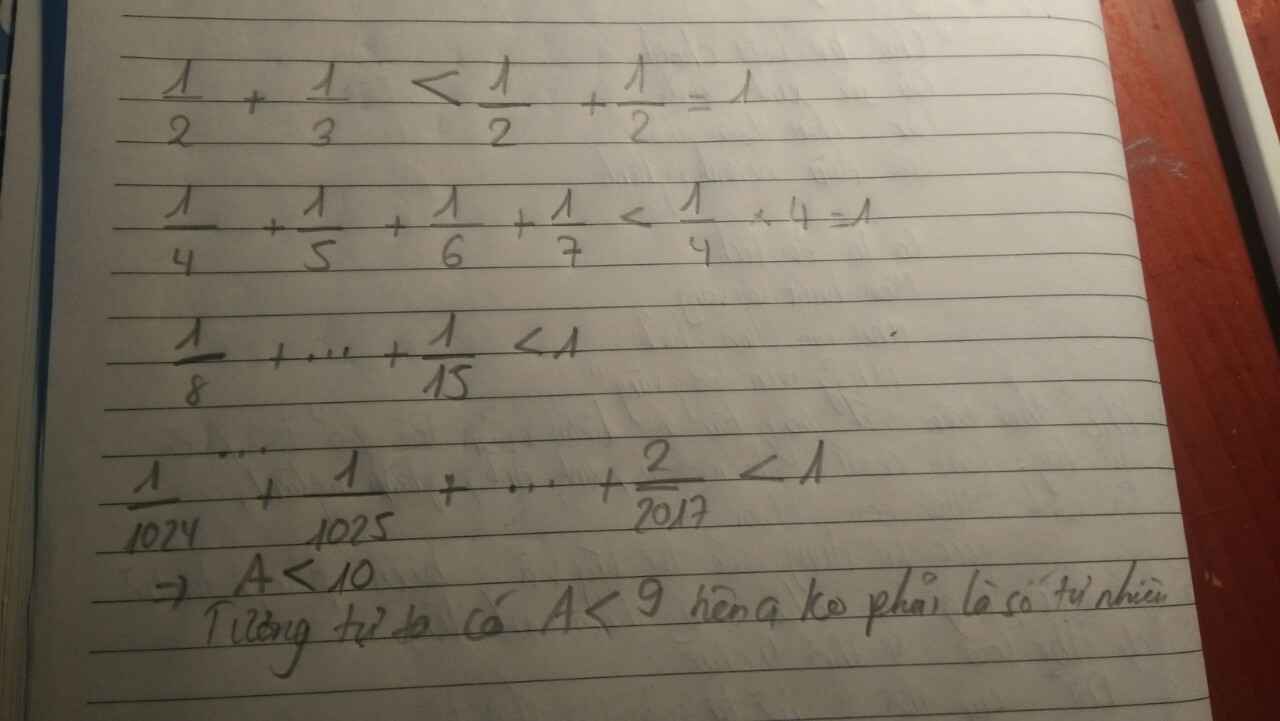
Ta có
1/2 =1/1.2
1/3 > 1/2 .3
1/4 > 1/3.4
......
1/50 > 1/49.50
A >1/1.2+1/2.3+1/3.4+...+1/49.50
A>1/1-1/2+1/2-1/3+...+1/49-1/50
A>1/1-1/50=49/50
vậy a<1
a có thể bằng 1 mà bn ê