Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biến cố chọn được 3 quả cân có tổng trọng lượng không vượt quá 9 kg.
Suy ra A có các trường hợp sau:
A = { (1, 2, 3); (1, 2, 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); (2, 3, 4)}
⇒P=7C83=18
Vậy xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg là:

Đáp án C
Các trường hợp thuận lợi là (6;2;1), (5;2;1), (5;2;1), (4;3;2), (4;3;1), (4;2;1), (3;2;1).
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8 .

Đáp án C
Số phần tử của không gian mẫu là số các tổ hợp chập 3 của 8 phần tử
![]()
Gọi A là biến cố “Lấy được 3 quả cân có tổng trọng lượng không vượt quá 9kg”
![]()
n(A) = 7
Xác suất xảy ra biến cố A là:
P ( A ) = 7 56 = 1 8 a

Đáp án D
Chọn ngẫu nhiên 3 quả cân từ 8 quả cân có ![]() cách.
cách.
Suy ra ![]()
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A={(1;2;3), (1;2;4), (1;2;6), (1;3;4), (1;3;5), (2;3;4)}
Suy ra n(A)=7
Vậy xác suất cần tìm là
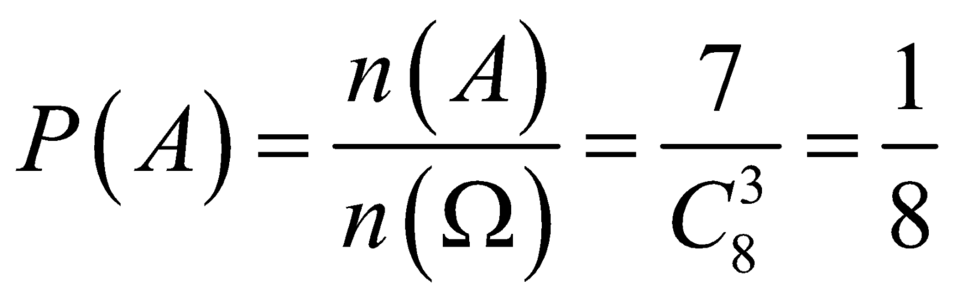

Đáp án C
Chọn ra 8 tấm thẻ 1 cách ngẫu nhiên có ![]() cách
cách
Trong 20 tấm thẻ có 10 tấm mang số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có: ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có ![]() cách.
cách.
Vậy xác suất cần tìm là
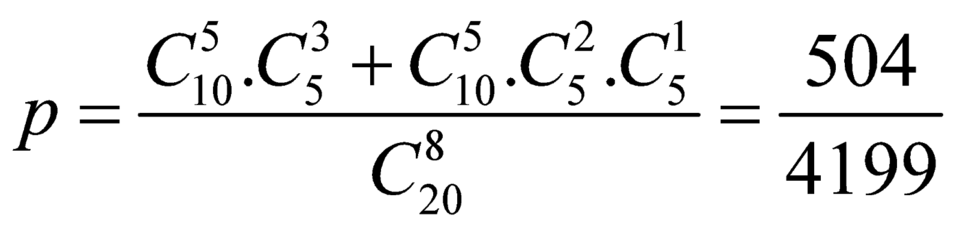
Lời giải:
Chọn ngẫu nhiên 3 quả cân trong số 8 quả cân, có $C^3_8=56$ cách chọn
Chọn 3 quả cân mà trọng lượng không vượt quá 9 kg có các TH sau:
$(1,2,3); (1,2,4); (1,2,5); (1,2,6); (1,3,4); (1,3,5); (2,3,4)$ (có 7 cách chọn)
Do đó xác suất để chọn được 3 quả cân có trọng lượng không vượt quá 9kg là: $\frac{7}{56}=\frac{1}{8}$