Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta gọi 6 điểm nằm trên đường tròn là A 1 , A 2 , A 3 , A 4 , A 5 , A 6 . Bằng bút xanh và đỏ ta nối A1 với 5 điểm còn lại ta được 5 đoạn thẳng có hai màu xanh hoặc đỏ.
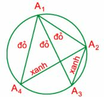
Theo nguyên lý Điríchlê có ít nhất 3 đoạn thẳng cùng màu. Không làm mất tính tổng quát, ta nối 3 đoạn A 1 A 2 , A 1 A 3 , A 1 A 4 bằng bút màu đỏ. Ta nối tiếp A 2 A 4 v à A 2 A 3 . Để tam giác A 1 A 2 A 3 và tam giác A 1 A 2 A 4 có 3 cạnh không cùng màu thì A 2 A 4 và A 2 A 3 phải tô màu xanh. Bây giờ ta tiếp tục nối A 3 A 4 , ta thấy A 3 A 4 được tô bằng bất kỳ màu xanh hoặc đỏ thì ta cũng được ít nhất một tam giác có 3 cạnh cùng màu (hoặc A 1 A 3 A 4 có 3 cạnh đỏ hoặc A 2 A 3 A 4 có 3 cạnh màu xanh).

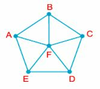
Tất cả các đỉnh A, B, C, D, E đều nối với đỉnh F nên đỉnh F phải tô màu khác với các đỉnh còn lại. Với 5 đỉnh còn lại thì A và C tô cùng một màu. B và D tô cùng một màu, E tô riêng một màu, như vậy cần ít nhất 3 màu để tô 5 đỉnh sao cho 2 đỉnh được nối bởi một cạnh được tô bởi 2 màu khác nhau. Vậy cần ít nhất 4 màu để tô 6 đỉnh của hình theo yêu cầu của đề bài.