Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
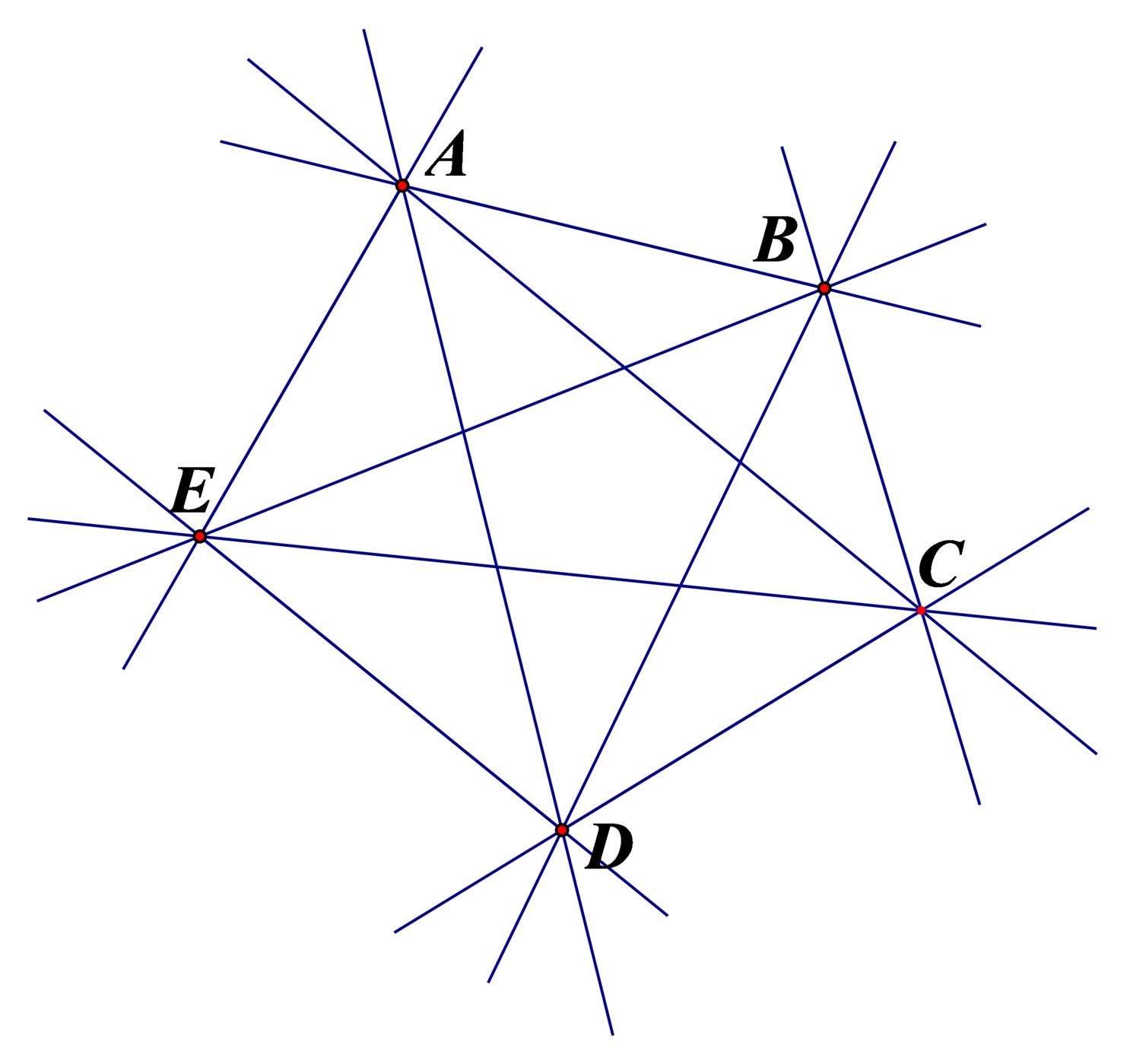
b) Có 10 đường thẳng đi qua 5 điểm nói trên. Đó là: AB , AC , AD , AE , BC , BD , BE , CD , CE , DE

Số đường thẳng vẽ đc là:
\(\frac{5\left(5-1\right)}{2}=10\)(đường thẳng)
Các đg thẳng đó là: AB;AC;AD;AE;BC;BD;BE;CD;CE;DE

nếu k có 4 điểm thẳng hàng thì ta có:
100x99:2=4950 (đường thẳng)
do có 4 điểm thẳng hàng nên ta chỉ vẽ đc 1 đường thẳng với 4 điểm đó
=> Có tất cả :
4950-(1x4)=4946 ( đường thẳng)
d/s:.....
Nếu không có 4 điểm thẳng hàng thì ta có:
100 x 99 : 2 = 4950 ( đường thẳng )
Do có 4 điểm thẳng hàng nên ta chỉ vẽ đươccj 1 đường thẳng với 4 điểm đó.
Có tất cả số đường thẳng là:
4950 - ( 1 x 4 ) = 4946 ( đường thẳng )
Đáp số: 4946 đường thẳng

Cứ 1 điểm sẽ tạo với 5 - 1 điểm còn lại 5 - 1 (đường thẳng)
Với 5 điểm sẽ tạo được số đường thẳng là:
(5-1)\(\times\) 5 ( đường thẳng)
Theo cách tính trên mỗi đường thẳng được tính hai lần vậy số đường thẳng được tạo là:
(5-1)\(\times\) 5 : 2 = 10 ( đường thẳng)
b, Kể tên các đường thẳng đó lần lượt là:
AB; AC; AD; AE; BC; BD; BE; CD; CE; DE

a) Vẽ được 10 đường thẳng. Các đường thẳng đó là AB, AC, AD, AE, BC, BD, BE, CD, CE, DE.
b) Vẽ được \(\dfrac{n\left(n-1\right)}{2}\) đường thẳng.
c) \(\dfrac{n\left(n-1\right)}{2}\)=28 \(\Rightarrow\) n=8.
Vậy có 8 điểm phân biệt cho trước thỏa yêu cầu đề bài.
Cứ 1 điểm với 1 điểm khác ta vẽ được 1 đường thẳng
Cứ 1 điểm với 4 điểm còn lại ta được 4 đường thẳng
Làm như vậy với 5 điểm ta được 4.5=20( đường thẳng)
Tuy nhiên số đường thẳng đã được tính 2 lần
Vậy số đường thẳng thật sự là 20:2=10