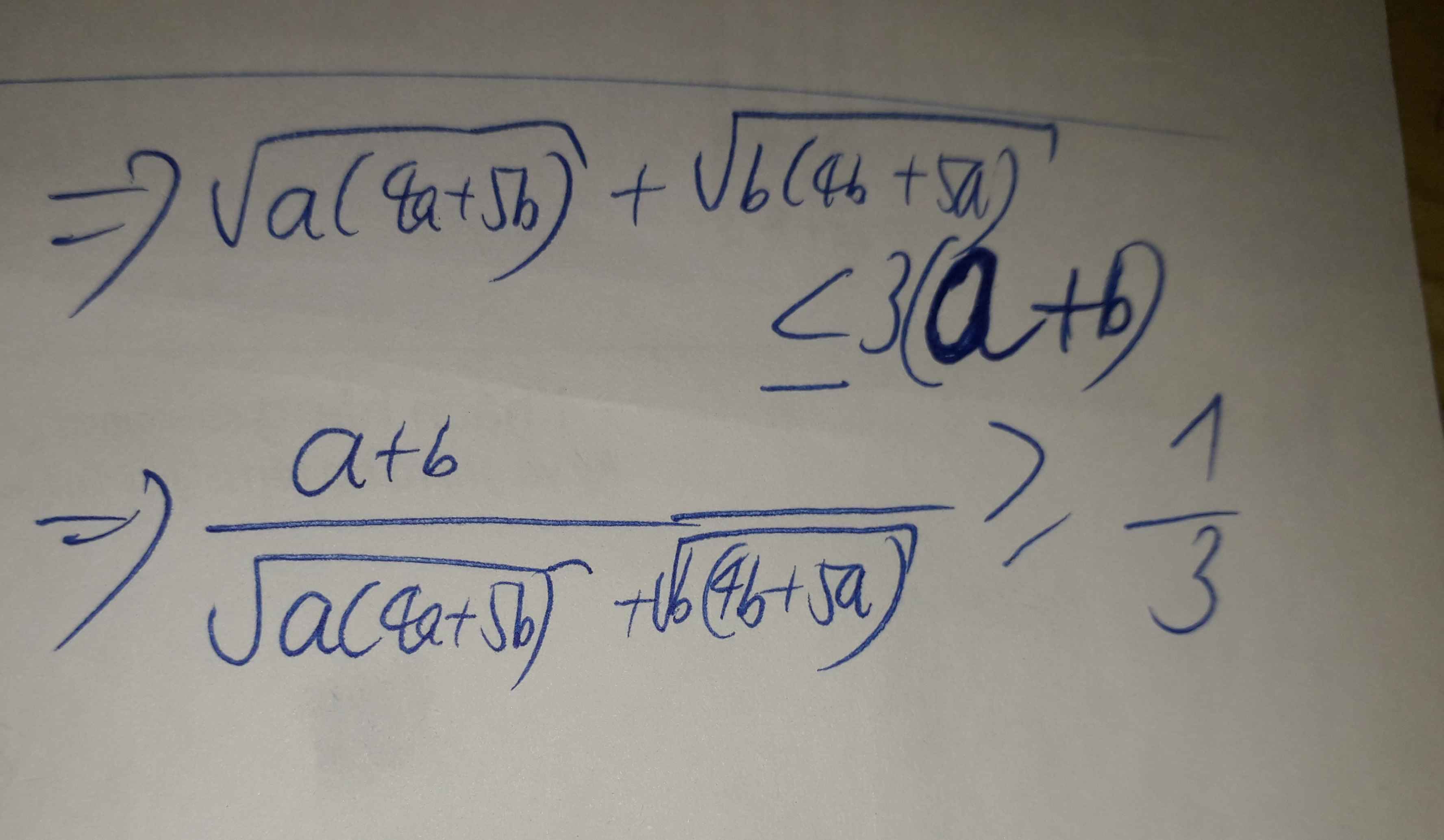Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo BĐT Cauchy: \(\left\{{}\begin{matrix}\sqrt{ab}\le\dfrac{a}{4}+b\\\sqrt[3]{abc}\le\dfrac{1}{3}\left(\dfrac{a}{4}+b+4c\right)\end{matrix}\right.\)
\(\Rightarrow a+\sqrt{ab}+\sqrt[3]{abc}\le a+\dfrac{a}{4}+b+\dfrac{1}{3}\left(\dfrac{a}{4}+b+4c\right)=\dfrac{4}{3}\left(a+b+c\right)\)
\(\Rightarrow P\ge\dfrac{1346}{\dfrac{4}{3}\left(a+b+c\right)}-\dfrac{2019}{\sqrt{a+b+c}}=\dfrac{2019}{2\left(a+b+c\right)}-\dfrac{2019}{\sqrt{a+b+c}}\)
\(\Rightarrow\dfrac{2P}{2019}\ge\dfrac{1}{a+b+c}-\dfrac{2}{\sqrt{a+b+c}}=\left(\dfrac{1}{\sqrt{a+b+c}}\right)^2-2.\dfrac{1}{\sqrt{a+b+c}}+1-1\)
\(\Rightarrow\dfrac{2P}{2019}\ge\left(\dfrac{1}{\sqrt{a+b+c}}-1\right)^2-1\ge-1\)
\(\Rightarrow P\ge\dfrac{-2019}{2}\)
\(\Rightarrow P_{min}=\dfrac{-2019}{2}\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\dfrac{a}{4}=b=4c\\\dfrac{1}{\sqrt{a+b+c}}-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{16}{21}\\b=\dfrac{4}{21}\\c=\dfrac{1}{21}\end{matrix}\right.\)