Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(P=a^2+b^2+c^2\)
\(\Rightarrow P+2=a^2+b^2+c^2+2\left(ab+bc+ac\right)\)
\(\Rightarrow P+2=\left(a+b+c\right)^2\ge0\)
\(\Rightarrow P\ge-2\)
Vậy MinP = -2 tại a + b + c = 0 .
Mik thấy a,b,c>0 \(\Rightarrow a+b+c>0\)
\(\Rightarrow2P-2=2a^2+2b^2+2c^2-2ab-2bc-2ca=\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) \(\Rightarrow2P\ge2\Rightarrow P\ge1\) Dấu bằng xảy ra \(\Leftrightarrow a=b=c=\dfrac{\sqrt{3}}{3}\) Vậy...

c1:áp dụng bđt AM-GM:
\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)
=> đáp án A
c2: tương tự c1 . đáp án b
3.
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)
Đáp án A
4.
\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)
Đáp án A


Đặt \(\left(a+1;b+1;c+1\right)=\left(x;y;z\right)\Rightarrow1\le x\le y\le z\le2\)
\(B=\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{y}{x}+\dfrac{z}{y}+\dfrac{z}{x}+\dfrac{x}{z}+3\) (1)
Do \(x\le y\le z\Rightarrow\left(z-y\right)\left(y-x\right)\ge0\)
\(\Leftrightarrow xy+yz\ge y^2+zx\)
\(\Leftrightarrow\dfrac{x}{z}+1\ge\dfrac{y}{z}+\dfrac{x}{y}\)
Tương tự: \(1+\dfrac{z}{x}\ge\dfrac{y}{x}+\dfrac{z}{y}\)
Cộng vế: \(2+\dfrac{x}{z}+\dfrac{z}{x}\ge\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{y}+\dfrac{y}{x}\) (2)
Từ (1); (2) \(\Rightarrow B\le2\left(\dfrac{x}{z}+\dfrac{z}{x}\right)+5\)
Đặt \(\dfrac{z}{x}=t\Rightarrow1\le t\le2\)
\(\Rightarrow B\le2\left(t+\dfrac{1}{t}\right)+5=\dfrac{2t^2+2}{t}+5=\dfrac{2t^2+2}{t}-5+10\)
\(\Rightarrow B\le\dfrac{2t^2-5t+2}{t}+10=\dfrac{\left(t-2\right)\left(2t-1\right)}{t}+10\le10\)
\(B_{max}=10\) khi \(t=2\) hay \(\left(a;b;c\right)=\left(0;0;1\right);\left(0;1;1\right)\)

ta có \(T=\frac{1}{2}\left(1-\frac{a^2}{2+a^2}+1-\frac{b^2}{2+b^2}+1-\frac{c^2}{2+c^2}\right)=\frac{1}{2}\left[3-\left(\frac{a^2}{2+a^2}+\frac{b^2}{2+b^2}+\frac{c^2}{2+c^2}\right)\right]\)
ta chứng minh rằng \(\frac{a^2}{2+a^2}+\frac{b^2}{2+b^2}+\frac{c^2}{2+c^2}\ge1\)khi đó ta sẽ có \(T\le1\)
thật vậy, áp dụng Bất Đẳng Thức Cauchy-Schwarz ta có \(\frac{a^2}{2+a^2}+\frac{b^2}{2+b^2}+\frac{c^2}{2+c^2}\ge\frac{\left(a+b+c\right)^2}{a^2+b^2+c^2+6}\)
ta cần chứng minh rằng \(\frac{\left(a+b+c\right)^2}{a^2+b^2+c^2+6}\ge1\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge a^2+b^2+c^2+6\)
\(\Leftrightarrow ab+bc+ca\ge3\)
thật vậy, từ giả thiết ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\le a+b+c\Leftrightarrow ab+bc+ca\le abc\left(a+b+c\right)\left(1\right)\)
mà \(abc\left(a+b+c\right)\le\frac{\left(ab+bc+ca\right)^2}{3}\)
từ (1) ta có \(\frac{ab+bc+ca}{3}\le\frac{\left(ab+bc+ca\right)^2}{3}\Leftrightarrow ab+bc+ca\ge3\left(đpcm\right)\)
vậy maxT=1 khi a=b=c=1

\(F=\left(a+b\right)^3-3ab\left(a+b\right)+ab=1-2ab\)
Ta có F đạt giá trị nhỏ nhất khi -2ab đạt giá trị nhỏ nhất.
Vì \(a+b=1\) có tổng không đổi nên \(-2ab\) đạt giá trị
nhỏ nhất khi ab đạt giá trị lớn nhất <=> a = b = 1/2
Thay a = b = 1/2 vào F tính được min F.
Ta có : F = (a+b)(a2 –ab+b2) +ab
Thay a+ b =1 vào F ta được F = a2 – ab +b2 + ab
F = a2 +b2 F = (a+b)2 – 2ab
F = 1 – 2ab Do a+b =1 ⇔ a = 1-b
thay vào F ta có : F = 1- 2(1-b)b F = 1 -2b+2b2 F = 2(b2 – b+41) + 21 F = 2(b -21)2 +21≥21
Với mọi b Dấu “ = ” xảy ra khi : b -21 = 0 ⇔ b =21 và a =21 Vậy Min F = 21 Khi a =b = 21
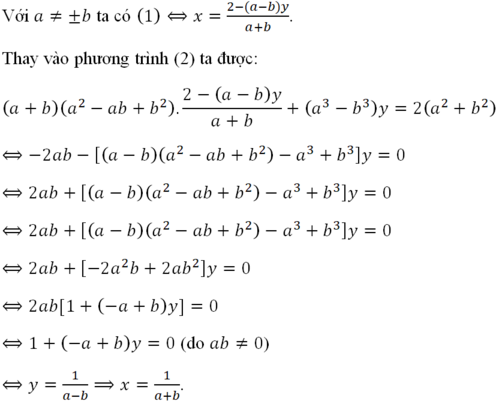
\(\left(a^3+b^3\right)\left(a+b\right)=ab\left(1-a\right)\left(1-b\right)\)
\(\Leftrightarrow\left(1-a\right)\left(1-b\right)=\left(\dfrac{a^2}{b}+\dfrac{b^2}{a}\right)\left(a+b\right)\ge\left(a+b\right)^2\ge4ab\)
\(\Rightarrow1+ab-4ab\ge a+b\ge2\sqrt{ab}\)
\(\Rightarrow3ab+2\sqrt{ab}-1\le0\)
\(\Leftrightarrow\left(\sqrt{ab}+1\right)\left(3\sqrt{ab}-1\right)\le0\)
\(\Leftrightarrow ab\le\dfrac{1}{9}\)
Bạn chuyển vế kiểu gì vậy