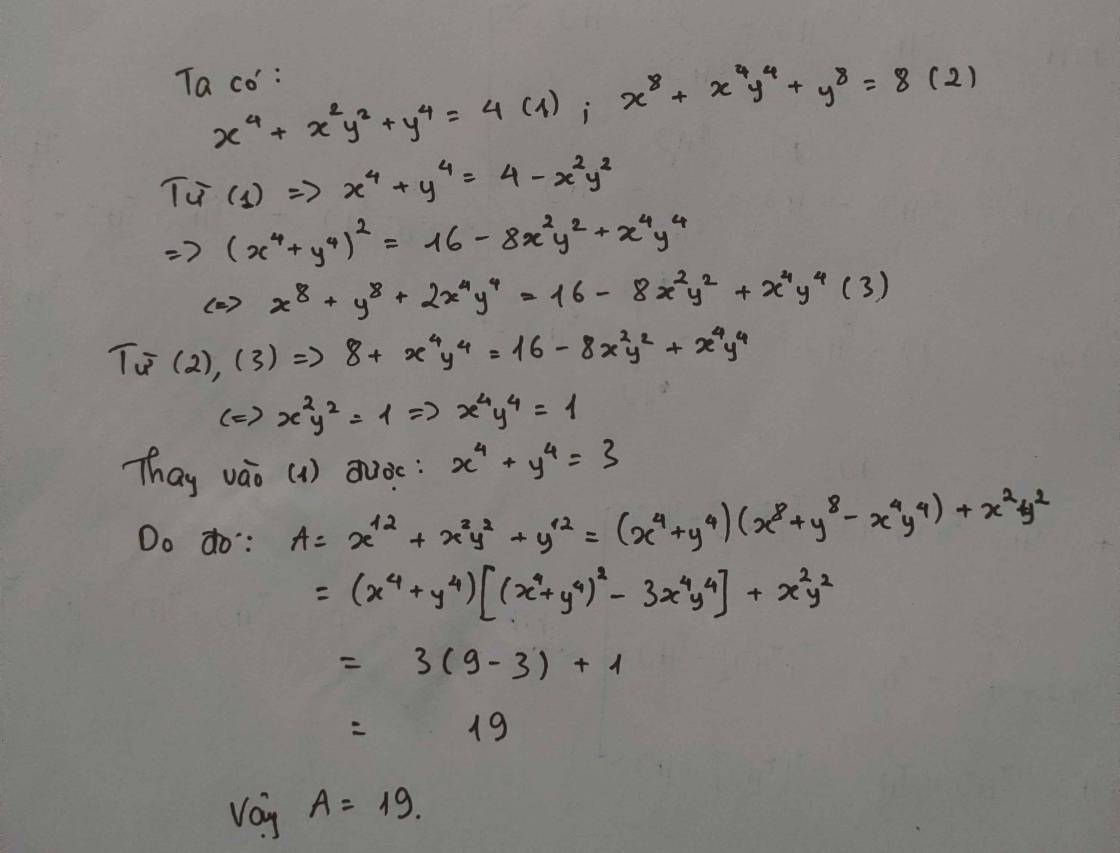KD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
JF
0
B
6 tháng 7 2023
Từ x8+x4y4+y8=(x4+y4)2-x4y4=(x4+y4-x2y2) (x4+y4+x2y2)=4(x4+y4-x2y2) =8
=>(x4+y4-x2y2)=2=>x4+y4=2+x2y2 kết hợp với x4+y4+x2y2=4
=> 2+x2y2+x2y2=4 => x2y2=1 (x4y4 sẽ = 1 nốt ) => x4+y4=3 và x8+y8=7
Xét (x4+y4)3=x12+y12+3x4y4(x4+y4)=x12+y12+3.1.3=33=27
=>x12+y12=18=> A = 18+1=19
TM
0
KH
0
HX
0
HP
2
NN
28 tháng 3 2017
Giải:
Cộng \(1\) vào \(2\) vế của 3 PT ta được:
\(\left(x+1\right)\left(y+1\right)=4\)
\(\left(y+1\right)\left(z+1\right)=9\)
\(\left(z+1\right)\left(x+1\right)=16\)
Nhân 2 PT bất kỳ rồi chia cho cái còn lại ta được:
\(\left(x+1\right)^2=4.\frac{16}{9}=\frac{64}{9}\Rightarrow x+1=\sqrt{\frac{64}{9}}\Rightarrow x=\frac{5}{3}\) (do \(x\) dương)
\(\left(y+1\right)^2=4.\frac{9}{16}=\frac{9}{4}\Rightarrow y+1=\sqrt{\frac{9}{4}}\Rightarrow y=\frac{1}{2}\) (do \(y\) dương)
\(\left(z+1\right)^2=9.\frac{16}{4}=36\Rightarrow z+1=\sqrt{36}\Rightarrow z=5\) (do \(z\) dương)
\(\Rightarrow P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{43}{6}\)
Vậy \(P=\frac{43}{6}\)
