Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
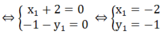
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).

Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
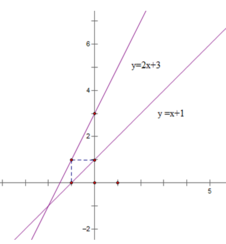
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)

b: y=mx-2x+3
Điểm mà (d) luôn đi qua có tọa độ là:
x=0 và y=-2*0+3=3

Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2