Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
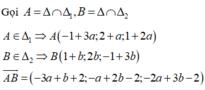
![]()

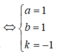
Ta có A(2;3;3); B(2;2;2)
Δ đi qua điểm A(2;3;3) và có vectơ chỉ phương A B → = 0 ; - 1 ; 1
Vậy phương trình của ∆ là x = 2 y = 3 - t z = 3 - t

Câu 2)
Giả sử tồn tại MP cố định đó. Gọi PTMP mà \((d_k)\) luôn đi qua là
\((P):a(x-3)+b(y+1)+c(z+1)=0\) $(1)$
Ta chỉ cần xác định được \(a,b,c\) nghĩa là đã chứng minh được sự tồn tại của mặt phẳng cố định đó.
Vì \(d_k\in (P)\forall k\Rightarrow \overrightarrow{u_{d_k}}\perp \overrightarrow {n_P}\)
\(\Rightarrow a(k+1)+b(2k+3)+c(1-k)=0\) với mọi $k$
\(\Leftrightarrow k(a+2b-c)+(a+3b+c)=0\) với mọi $k$
\(\Leftrightarrow \left\{\begin{matrix} a+2b-c=0\\ a+3b+c=0\end{matrix}\right.\)
Từ đây ta suy ra \(a=\frac{-5b}{2}\) và \(c=\frac{-b}{2}\)
Thay vào \((1)\) và triệt tiêu \(b\) (\(b\neq 0\) bởi vì nếu không thì \(a=c=0\) mặt phẳng không xác định được)
\(\Rightarrow (P): -5x+2y-z+16=0\)
\((d_k)\parallel (6x-y-3z-13=0(1),x-y+2z-3=0(2))\)
\(\Leftrightarrow \overrightarrow {u_{d_k}}\perp \overrightarrow {n_1},\overrightarrow{n_2}\)\(\Rightarrow \overrightarrow{u_{d_k}}\parallel[\overrightarrow{n_1},\overrightarrow{n_2}]\)
Mà \(\overrightarrow{n_1}=(6,-1,-3);\overrightarrow{n_2}=(1,-1,2)\)
\(\Rightarrow \overrightarrow{u_{d_k}}\parallel(-5,-15,-5)\) hay \(\frac{k+1}{-5}=\frac{2k+3}{-15}=\frac{1-k}{-5}\Rightarrow k=0\)
Câu 1 mình đặt ẩn nhưng dài quá nhác viết, với lại mình thấy nó không hay và hiệu quả. Mình nghĩ với cách cho giá trị AB,CD cụ thể thế kia thì chắc chắn có cách nhanh gọn hơn. Nếu bạn có lời giải rồi thì post lên cho mình xem ké với.

Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)

Bài 1:
Gọi tọa độ của \(A=(0,0,a)\) và \(B=(m,n,p)\)
Vì $(P)$ vuông góc với $(d)$ nên \(\overrightarrow {n_P}=\overrightarrow {u_d}=(2,-1,1)\) kết hợp với $(P)$ chứa $A$ nên PTMP: \((P):2x-y+z-a=0\)
Ta có \(B\in (P)\Rightarrow 2m-n+p-a=0(1)\)
Mặt khác \(B\in (d')\Rightarrow \frac{m-1}{1}=\frac{n}{2}=\frac{p+2}{1}=t\Rightarrow \left\{\begin{matrix} m=t+1\\ n=2t\\ p=t-2\end{matrix}\right.\)
Thay vào $(1)$ ta thu được $t=a$
\(\Rightarrow AB=\sqrt{m^2+n^2+(p-a)^2}=\sqrt{(a+1)^2+(2a)^2+4}=\sqrt{5a^2+2a+5}\geq \frac{2\sqrt{30}}{5}\Leftrightarrow a=\frac{-1}{5}\)
Có nghĩa là để $AB$ min thì $a=\frac{-1}{5}$
Vậy PTMP: \(2x-y+z-\frac{1}{5}=0\)
Câu 2:
Thay toạ độ $A$ và $B$ vào $(P)$ có \([3.1-4(-1)+2-1](3.3-4.0+1-1)>0\) nên $A,B$ cùng phía so với $(P)$
Lấy $A'$ đối xứng với $A$ qua $(P)$ \(\Rightarrow MA=MA'\Rightarrow MA+MB=MA'+MB\geq A'B\)
Do đó \((MA+MB)_{\min}\Leftrightarrow A',M,B\) thẳng hàng
Biểu thị $(d)$ là đường thẳng chứa đoạn $AA'$.
Hiển nhiên \((d)\perp (P)\Rightarrow \overrightarrow{u_d}=\overrightarrow {n_P}=(3,-4,1)\)
Kết hợp với $A\in (d)$ nên \(d:\frac{x-1}{3}=\frac{y+1}{-4}=\frac{z-2}{1}=t\)
Khi đó gọi \(H\equiv AA'\cap (P)\). Dễ có \(H=(\frac{1}{13},\frac{3}{13},\frac{22}{13})\)
Lại có $H$ là trung điểm của $AA'$ nên tọa độ của $A'$ là
\(\left\{\begin{matrix} x_{A'}=2x_H-x_A=\frac{-11}{13}\\ y_{A'}=2y_H-y_A=\frac{19}{13}\\ z_{A'}=2z_H-z_A=\frac{18}{13}\end{matrix}\right.\)
Khi đó ta dễ dàng viết được PTĐT chứa $A'B$ là \(\frac{13(x-3)}{50}=\frac{13y}{19}=\frac{13(z-1)}{5}\)
Tọa độ của $M$ là nghiệm của hệ
\(\left\{\begin{matrix} \frac{13(x-3)}{50}=\frac{13y}{19}=\frac{13(z-1)}{5}\\ 3x-4y+z-1=0\end{matrix}\right.\Rightarrow M(\frac{-213}{79},\frac{-171}{79},\frac{34}{79})\)
.

\(\left\{{}\begin{matrix}\overrightarrow{n_{\left(P1\right)}}=\left(1;-1;1\right)\\\overrightarrow{n_{\left(P2\right)}}=\left(3;2;-12\right)\end{matrix}\right.\) \(\Rightarrow\)\(\left[\overrightarrow{n_{\left(P1\right)}};\overrightarrow{n_{\left(P2\right)}}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Chọn \(\overrightarrow{n_{\left(p\right)}}=\left(2;3;1\right)\) là 1 vtpt của (P)
Phương trình (P): \(2x+3y+z=0\)
Câu 2:
\(\left\{{}\begin{matrix}\overrightarrow{u_d}=\left(2;1;1\right)\\\overrightarrow{u_{d'}}=\left(1;-2;1\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right]=\left(3;-1;-5\right)\)
\(\Rightarrow\) Chọn \(\overrightarrow{n_{\alpha}}=\left(3;-1;-5\right)\) là một vtpt của \(\left(\alpha\right)\)
Phương trình \(\left(\alpha\right)\):
\(3\left(x-0\right)-1\left(y-1\right)-5\left(z-2\right)=0\)
\(\Leftrightarrow3x-y-5z+11=0\)

Câu 1:
\(\overrightarrow{MN}=\left(3;-1;-4\right)\Rightarrow\) pt mặt phẳng trung trực của MN:
\(3\left(x-\frac{7}{2}\right)-\left(y-\frac{1}{2}\right)-4\left(z-2\right)=0\Leftrightarrow3x-y-4z-2=0\)
\(\overrightarrow{PN}=\left(4;3;-1\right)\Rightarrow\) pt mp trung trực PN: \(4x+3y-z-7=0\)
\(\Rightarrow\) Phương trình đường thẳng giao tuyến của 2 mp trên: \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=t\end{matrix}\right.\)
\(\Rightarrow I\left(1+c;1-c;c\right)\) \(\Rightarrow\overrightarrow{NI}=\left(c-4;1-c;c\right)\)
\(d\left(I;\left(Oyz\right)\right)=IN\Rightarrow\left|1+c\right|=\sqrt{\left(c-4\right)^2+\left(1-c\right)^2+c^2}\)
\(\Leftrightarrow\left(c+1\right)^2=3c^2-10c+17\)
\(\Leftrightarrow2c^2-12c+16=0\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\)
Mà \(a+b+c< 5\Rightarrow\left(1+c\right)+\left(1-c\right)+c< 5\Rightarrow c< 3\Rightarrow c=2\)
Câu 2:
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=t\\z=2-t\end{matrix}\right.\) \(\Rightarrow C\left(-1+2n;n;2-n\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2n;n-3;1-n\right)\\\overrightarrow{AB}=\left(1;-1;-2\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(3n-7;-3n-1;3n-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(3n-7\right)^2+\left(-3n-1\right)^2+\left(3n-3\right)^2}=4\sqrt{2}\)
\(\Leftrightarrow27n^2-54n+27=0\Rightarrow n=1\)
\(\Rightarrow C\left(1;1;1\right)\Rightarrow m+n+p=3\)

