Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,có \(R1//R2//R3\)
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{10}+\dfrac{1}{20}+\dfrac{1}{20}\)
\(=>Rtd=5\left(om\right)\)
\(b,=>Im=\dfrac{U}{Rtd}=\dfrac{12}{5}=2,4A\)
\(=>U=U123=U1=U2=U3=12V\)
\(=>\left\{{}\begin{matrix}I1=\dfrac{U1}{R1}=\dfrac{12}{10}=1,2A\\I2=\dfrac{U2}{R2}=\dfrac{12}{20}=0,6A\\I3=\dfrac{U3}{R3}=\dfrac{12}{20}=0,6A\end{matrix}\right.\)

a) Điện trở tương đương của toàn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{4.6}{4+6}=2,4\left(\Omega\right)\)
b) Có : \(U=U_1=U_2=6\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện trở R1 :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{6}{4}=1,5\left(A\right)\)
Cường độ dòng điện qua mạch chính :
\(I=\dfrac{U}{R_{tđ}}=\dfrac{6}{2,4}=2,5\left(A\right)\)
Chúc bạn học tốt

a. Điên trở tương đương của đoạn mạch này là :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.12}{60+12}=10\Omega\)
b. CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R}=\dfrac{2,4}{10}=0,24A\)
Vì \(R_1\)//\(R_2\) nên :
\(U=U_1=U_2=2,4V\)
CĐDĐ qua các đoạn mạch rẽ là :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{2,4}{60}=0,04A\)
\(\Rightarrow I_2=0,24-0,04=0,2A\)
c. Vì điện trở \(R_3\) nt ( \(R_1\)//\(R_2\)) nên điện trở tương đương toàn mạch là :
\(R_{123}=R_{12}+R_3=10+16=26\Omega\)
\(\Rightarrow\) CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R_{123}}=\dfrac{2,4}{26}\approx0,1A\)
Vậy : a. Điện trở tương đương của đoạn mạch \(R_1\)//\(R_2\) là \(10\Omega\)
b. I = 0,24A ; \(I_1=0,04A\) ; \(I_2=0,2A\)
c. \(I_{123}\) = 0,1A

a. Hiệu điện thế ở 2 đầu đoạn mạch là
\(U=R_1I_1=12.0,2=2,4\) (V)
b. Dòng điện đi qua \(R_2\) và \(R_3\) lần lượt là
\(I_2=\dfrac{U}{R_2}=0,24\) (A)
\(I_3=\dfrac{U}{R_3}=0,16\) (A)
Điện trở tương đương của mạch là
\(\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\Rightarrow R=4\left(\Omega\right)\)
Cường độ dòng điện qua mạch chính là
\(I=\dfrac{U}{R}=0,6\) (A)
Chúc em học tốt.

a. Điện trở tương đương của đoạn mạch:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=14,4\left(\Omega\right)\)
b. Cường độ dòng điện qua mạch chính là:
\(I=\dfrac{U}{R_{tđ}}=1\left(A\right)\)
Cường độ dòng điện qua điện trở R1 là: \(I_1=\dfrac{U}{R_1}=0,4\left(A\right)\)
Cường độ dòng điện qua điện trở R2 là: \(I_2=I-I_1=0,6\left(A\right)\)

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{3}{10}\Omega\)
\(\Rightarrow R_{tđ}=\dfrac{10}{3}\Omega\)
\(U_1=U_2=U_3=U=12V\)
\(I=\dfrac{U}{R}=\dfrac{12}{\dfrac{10}{3}}=3,6A\)
\(I_1=I_2=I_3=\dfrac{U_1}{R_1}=\dfrac{12}{10}=1,2A\)
Nếu mắc nối tiếp:
\(R_{tđ}=R_1+R_2+R_3=10+10+10=30\Omega\)
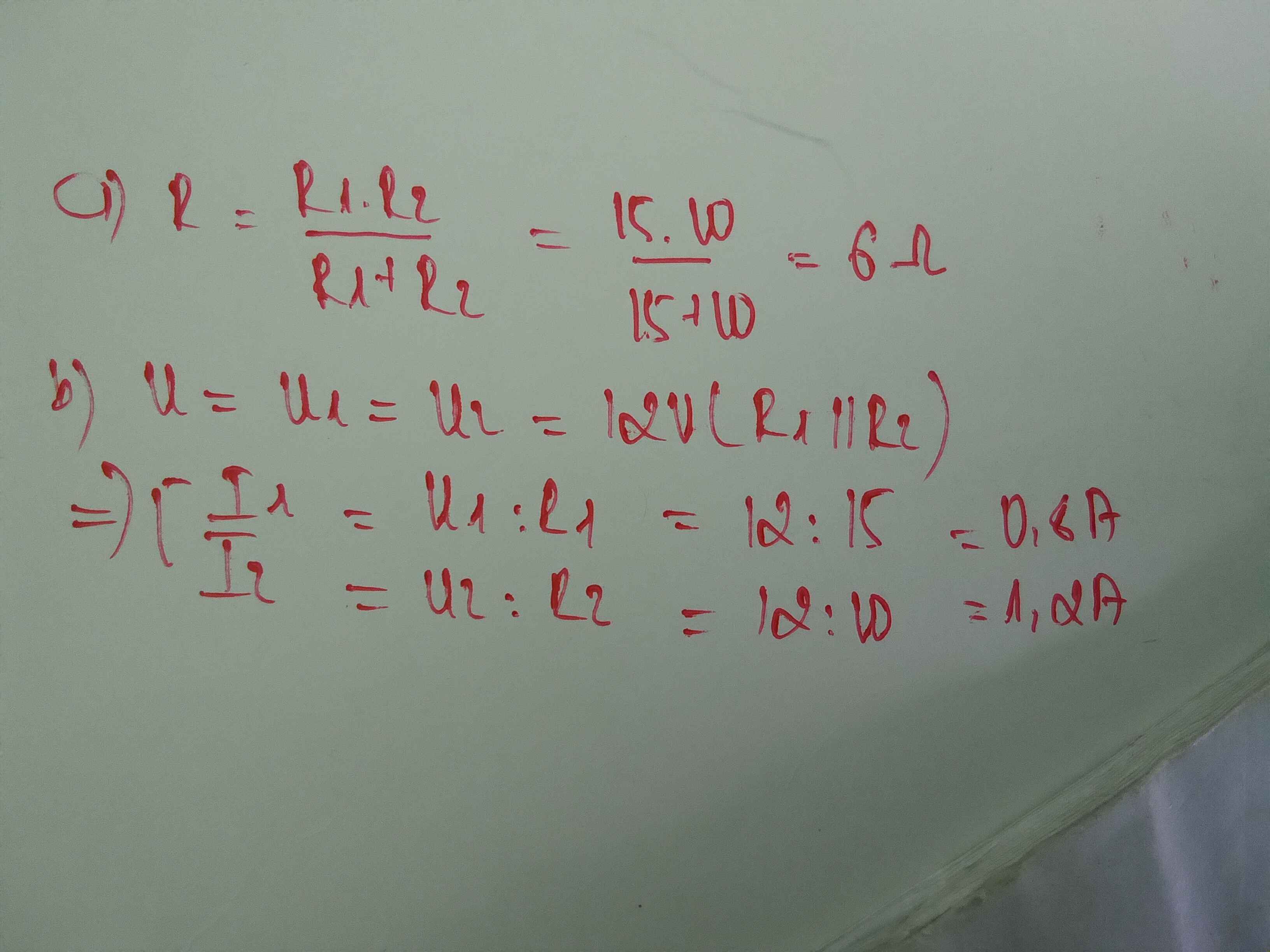
a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.15}{10+15}=6\left(\Omega\right)\)
b. \(U=U1=U2=12\left(V\right)\)(R1//R2)
\(\left[{}\begin{matrix}I=U:R=12:6=2\left(A\right)\\I1=U1:R1=12:10=1,2\left(A\right)\\I2=U2:R2=12:15=0,8\left(A\right)\end{matrix}\right.\)
I3 đâu ra vậy?