Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài ta có : M là điểm chính giữa cung AB nên cung AM = cung MB
Xét đường tròn (O) có:
+) MCD là góc nội tiếp chắn cung DM⇒ˆMCD=\(\frac{1}{2}\)sđ cung DM. (1)
+) ˆAED là góc có đỉnh nằm trong đường tròn chắn cung MB và cung AD
=> ^MCD = \(\frac{1}{2}\)(sđ AD + sđ MB) =\(\frac{1}{2}\)(sđ AD +sđ MA) = \(\frac{1}{2}\)sđ DM (2)
Từ (1) và (2) => ^MCD =^AED=\(\frac{1}{2}\)sđ DM
Xét tứ giác DEPC có : ^MCD =^AED (cmt)
=> đpcm

Ta có: \(\widehat{C_1}=\dfrac{1}{2}sđ\stackrel\frown{DM}\)
Mặt khác: \(\widehat{E_1}=\dfrac{sđ\stackrel\frown{BM}+sđ\stackrel\frown{AD}}{2}\)
\(=\dfrac{sđ\stackrel\frown{AM}+sđ\stackrel\frown{AD}}{2}=\dfrac{1}{2}sđ\stackrel\frown{DM}\)(Vì M là điểm chính giữa \(\stackrel\frown{AB}\) \(\Rightarrow\stackrel\frown{AM}=\stackrel\frown{BM}\))
\(\Rightarrow\widehat{C_1}=\widehat{E_1}\)
Vì \(\widehat{E_1}+\widehat{E_2}=180^o\Rightarrow\widehat{C_1}+\widehat{E_2}=180^o\) mà 2 góc đối nhau
=> tứ giác PEDC nội tiếp

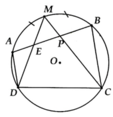
Ta có: A E D ^ = 1 2 s đ A D ⏜ + s đ M B ⏜
= 1 2 s đ D M ⏜ = M C D ^ => D E P ^ + P C D ^ = 180 0
=> PEDC nội tiếp

Đề bài bị thừa hai điểm M,N nhé bạn.
Gọi X,Y tương ứng là tiếp điểm của hai đường tròn \(\left(O_1\right),\left(O_2\right)\) với \(BC\). Ta có \(\Delta O_1XH\sim\Delta O_2YH\) (cùng là tam giác vuông cân). Suy ra \(\frac{O_1H}{O_2H}=\frac{r_1}{r_2}\) với \(r_1,r_2\) tương ứng là bán kính đường tròn nội tiếp hai tam giác \(\Delta AHB,\Delta CHA.\) Mà \(\Delta AHB\sim\Delta CHA\) nên \(\frac{r_1}{r_2}=\frac{AB}{CA}\to\frac{O_1H}{O_2H}=\frac{AB}{CA}\to\Delta O_1HO_2\sim\Delta BAC\) (c.g.c). Suy ra \(\angle ABC+\angle HO_2O_1=90^{\circ}.\)
Đến đây ta có \(\angle CO_2O_1+\angle O_1BC=\angle HO_2C+\angle HO_2O_1+\angle O_1BC\)
\(=180^{\circ}-\frac{\angle AHC+\angle ACH}{2}+\angle HO_2O_1+\angle O_1BC=180^{\circ}-\frac{180^{\circ}-\angle HAC}{2}+\angle HO_2O_1+\angle O_1BC\)
\(=90^{\circ}+\angle HO_2O_1+\angle ABC=180^{\circ}.\)
Vậy tứ giác \(BCO_1O_2\) nội tiếp.