Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔABE có BA=BE
nên ΔABE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔABE đều
c: Xét ΔABC vuông tại A có
\(\cos B=\dfrac{AB}{BC}\)
=>5/BC=1/2
hay BC=10(cm)
\(\Rightarrow\dfrac{x-1}{2011}-1+\dfrac{x-2}{2010}-1+\dfrac{x-3}{2009}-1=\dfrac{x-4}{2008}-1-2\)
\(\Rightarrow\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}=\dfrac{x-2012}{2008}-\dfrac{x-2012}{\left(x-2012\right)\div2}\)
\(\Rightarrow\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}-\dfrac{1}{2008}-\dfrac{1}{\left(x-2012\right)\div2}=0\)
Vì vế bên trên \(\ge0\)
\(x-2012=0\)
\(x=2012\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔAHC vuông tại H có \(\widehat{C}=45^0\)
nên ΔAHC vuông cân tại H
=>\(AH=HC=\dfrac{BC}{2}=\dfrac{5}{2}\sqrt{2}\left(cm\right)\)

a) Tam giác ABD vuông và tam giác EBD vuông đều có cạnh BD
Suy ra góc ABD = góc EBD
Vậy tam giác ABD = tam giác EBD
b) Ta có: AB=EB ( tam giác ABD = tam giác EBD )
Suy ra tam giác ABE cân tại B
Tam giác ABE cân tại B có góc EBA =60 độ
Suy ra tam giác ABE là tam giác đều
c) Tam giác ABC có góc CAB = 90 độ, góc CBA = 60 độ
Suy ra ACB = 30 độ
Suy ra tam giác ABC là nửa tam giác đều
Suy ra AB = 1/2 BC
Suy ra BC = 2AB = 2 . 5 = 10 cm
chúc bạn học tốt! ![]()
![]()
![]()
![]()


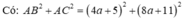

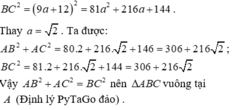

đk : a;b;c > 0
Theo bài ra ta có :
\(20a=15b=12c\Rightarrow\dfrac{20a}{60}=\dfrac{15b}{60}=\dfrac{12c}{60}\Rightarrow\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
đề thiếu rồi bạn
Đề thiếu đâu Tú