Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy \(I\)là trung điểm của \(AB\).
Khi đó \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\)
\(\overrightarrow{MA}.\overrightarrow{MB}=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)\left(\overrightarrow{MI}+\overrightarrow{IB}\right)=\overrightarrow{MI}.\overrightarrow{MI}+\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}\right)+\overrightarrow{IA}.\overrightarrow{IB}\)
\(=MI^2-\frac{a^2}{4}=2a^2\Leftrightarrow MI^2=\frac{9}{4}a^2\)
Suy ra \(M\)thuộc đường tròn tâm \(I\)bán kính \(\frac{3a}{2}\).

Chắc đề là: \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|=a\) ?
\(\left|\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\right|=a\)
\(\Leftrightarrow\left|4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right|=a\)
\(\Leftrightarrow4\left|\overrightarrow{MO}\right|=a\)
\(\Leftrightarrow MO=\dfrac{a}{4}\)
Tập hợp M là đường tròn tâm O bán kính \(\dfrac{a}{4}\)

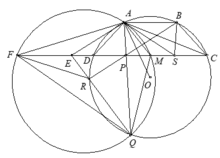
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.
Tập hợp điểm R thỏa mãn \(\left|\overrightarrow{RA}\right|=\left|\overrightarrow{AB}\right|\) là đường tròn tâm A bán kính AB
cảm ơn ạ