Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y,z là 3 phần chia ra từ N lần lượt tỷ lệ nghịch với 2,5,6
Theo đề bài, ta có:
x^2+y^2+z^2=1144 (1)
x+y+z=N. (2)
Gọi k là hằng số của hệ số nghịch đảo của x,y,z lần lượt là 2,5,6
Ta có:
x=k/2 ; y=k/5 ; z=k/6 (3)
Thay (3) vào (1) , ta được:
=>k^2/4+k^2/25+k^2/36=1144
=>225.k^2+36.k^2+25.k^2=1029600
=>286.k^2=1029600
=>k^2=1029600:286
=>k^2=3600
=>k=60
Thay k=60 vào (3),ta được:
x=30 ; y=12 ; z=10 (4)
Thay (4) vào (2),ta được:
N=30+12+10
Vậy N=52
Đ s: N=52

Gọi 3 phần dc chia của số N lần lượt là a, b, c
Theo bài ta có :
\(a^2+b^2+c^2=1144\)
\(2a=5b=6c\)
\(\Leftrightarrow\dfrac{2a}{30}=\dfrac{5b}{30}=\dfrac{6c}{30}\)
\(\Leftrightarrow\dfrac{a}{15}=\dfrac{b}{6}=\dfrac{c}{5}\)
\(\Leftrightarrow\dfrac{a^2}{225}=\dfrac{b^2}{36}=\dfrac{c^2}{25}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a^2}{225}=\dfrac{b^2}{36}=\dfrac{c^2}{25}=\dfrac{a^2+b^2+c^2}{225+36+25}=\dfrac{1144}{286}=4\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a^2}{225}=4\\\dfrac{b^2}{36}=4\\\dfrac{c^2}{25}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2=900\\b^2=144\\c^2=100\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=30\\a=-30\end{matrix}\right.\\\left[{}\begin{matrix}b=12\\b=-12\end{matrix}\right.\\\left[{}\begin{matrix}c=10\\c=-10\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(a,b,c\right)\) là \(\left(30,12,10\right);\left(-30,-12,-10\right)\)

Câu hỏi của Phạm Minh Phương t - Toán lớp 7 - Học toán với OnlineMath
Câu 1:
Gọi ba phần được chia từ số 470 lần lượt là x, y, z
Có: Ba phần tỉ lệ nghịch với 3, 4, 5
⇒x3=y4=z5⇒x20=y15=z12⇒x3=y4=z5⇒x20=y15=z12 và x+y+z=470x+y+z=470
Áp dụng tính chất dãy tỉ số bằng nhau
x20=y15=z12=x+y+z20+15+12=47047=10x20=y15=z12=x+y+z20+15+12=47047=10
⇒\hept⎧⎨⎩x=200y=150z=120

Câu tương tự :
Gọi x,y,z là 3 phần chia ra từ A lần lượt tỉ lệ nghịch với 5, 2 và 4.
Theo đề bài, ta có: x^3 + y^3 + z^3 = 9512 (1)
x + y + z = A (2)
Gọi k là hằng số của hệ số nghịch đảo của x,y,z và 5,2,4.
Ta có x = k/5, y=k/2, z=k/4 (3)
Thay (3) vào (1) ta có:
k^3/5^3 + k^3/2^3 + k^3/4^3 = 9512
-> k^3/125 + k^3/8 + k^3/64 = 9512
-> 64*k^3 + (125*8)k^3 + 125*k^3 = 9512 * 125 * 64
-> (64 + 1000 + 125)* k^3 = 76096000
-> k^3 = 76090000 / 1189 = 64000 = 64 * 1000 = 4^3 * 10^3 = (4*10)^3
-> k = 40
Suy ra: x = k/5 = 8, y = k/2 = 20, z = k/4 = 10
Theo (2) ta suy ra A = x+y+z = 8+20+10 = 38

Gọi ba phần được chia ra từ số A lần lượt là x,y,z (x,y,z > 0)
Theo đề bài, ba phần tỉ lệ nghịch với các số nên ta có:
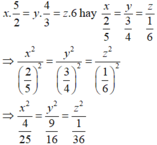
Tổng bình phương của ba phần là 24309 nên x 2 + y 2 + z 2 = 24309
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
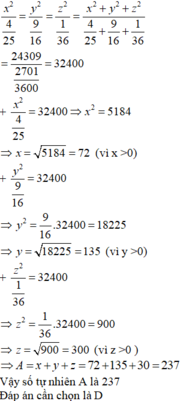

gọi 3 phần là x,y,z
Ta có : \(x:y:z=\frac{1}{5}:\frac{1}{2}:\frac{1}{4}=4:10:5\)hay \(\frac{x}{4}=\frac{y}{10}=\frac{z}{5}=k\)
suy ra : k3 = \(\frac{x^3}{64}=\frac{y^3}{1000}=\frac{z^3}{125}=\frac{x^3+y^3+z^3}{64+1000+125}=\frac{9512}{1189}=8\)
\(\Rightarrow k=2\)
\(\Rightarrow\frac{x+y+z}{4+10+5}=2\)suy ra : x + y + z = 2 . 19 = 38
Vậy A = 38
Gọi 3 phần là a,b,c
Ta có: \(\frac{a}{\frac{1}{5}}=\frac{b}{\frac{1}{2}}=\frac{c}{\frac{1}{4}}\Rightarrow\frac{a^3}{\frac{1}{125}}=\frac{b^3}{\frac{1}{8}}=\frac{c^3}{\frac{1}{64}}=\frac{a^3+b^3+c^3}{\frac{1}{125}+\frac{1}{8}+\frac{1}{64}}=\frac{9512}{\frac{1189}{8000}}=64000\)
\(\Rightarrow\frac{a^3}{\frac{1}{125}}=64000\Rightarrow a^3=512\Rightarrow a=8\)
\(\frac{b^3}{\frac{1}{8}}=64000\Rightarrow b^3=8000\Rightarrow b=20\)
\(\frac{c^3}{\frac{1}{64}}=64000\Rightarrow c^3=1000\Rightarrow c=10\)
Vậy A = a + b + c = 8 + 20 + 10 = 38