Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

.1 . Vẽ vòng tâm \(O\), bán kính \(R\). Gỉa sử \(R=1\)
2 . Từ 1 điểm \(B\)trên vòng tròn kẻ đường thẳng qua \(O\)và \(B\)
3 . Vẽ điểm \(D\)của \(OB\)
4 . Kẻ đường thăng vuông góc OB tại O , cắt vòng tròn qua hai điểm tại P
5 . Vẽ phân giác cuả ODP , cắt OP tại N
6 . Kẻ đường thẳng vuông góc với OP tại N cắt vòng tròn hai điểm tại P
Cái trên là ví dụ nha

1. Từ thước và compa, và góc 19 độ có sẵn, ta dựng lại được góc 19 độ.
2. ghép góc 19 độ liên tiếp 19 lần quang gốc tạo độ tạo thành 19* 19 =361 độ, trừ cho góc 360 độ, thành 1 độ

Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
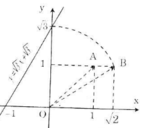
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
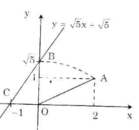
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
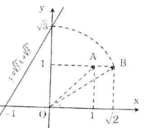
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
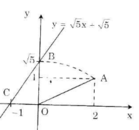
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
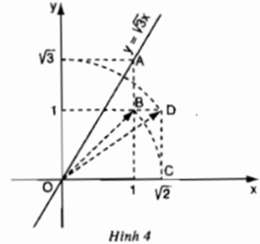
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
![]()
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
![]()
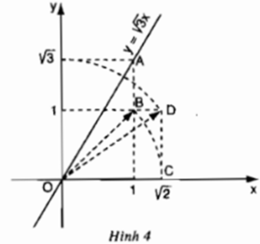
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.

- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
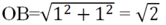
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
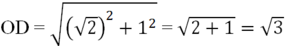
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.

* Phân tích
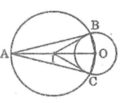
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán
Ta có: AB ⊥ OB ⇒ ∠ ABO = 90 °
AC ⊥ OC ⇒ ∠ ACO = 90 °
Tam giác ABO có ∠ ABO = 90 ° nội tiếp trong đường tròn đường kính AO và tam giác ACO có ∠ ACO = 90o nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
- Dựng I là trung điểm của OA
- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C
- Nối AB, AC ta được hai tiếp tuyến cần dựng
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ABO = 90 °
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ACO = 90 °
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).
Năm 1796, nhà toán học Carl Friedrich Gauss đã tìm được cách vẽ đa giác đều có 17 cạnh bằng thước thẳng và compa, bằng cách xem các đỉnh của đa giác trên vòng tròn như là nghiệm của phương trình số phức zn – 1 = 0.
face face nomi