AN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
.Nhưng khoảng từ pi/2 đến -pi/4 thì vẫn bao gồm đáp án A mà sao mình lại chọn ạ
TA
27 tháng 6 2021
TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 6 2023
Đường link tham khảo: Có nên "khoanh lụi" thi THPTQG hay không?
https://www.youtube.com/watch?v=gETeWVaK-E8
TL
22 tháng 6 2023
\(n\left(\Omega\right)=4^{50}\)
Nếu bạn An bị điểm liệt thì số câu đúng mà bạn chọn được bé hơn hoặc bằng 5, hay số câu sai lớn hơn hoặc bằng 45.
Gọi biến cố A: "bạn An không bị điểm liệt"
\(n\left(\overline{A}\right)=C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}\)
Xác suất để bạn An không bị điểm liệt
\(P\left(A\right)=1-\dfrac{n\left(\overline{A}\right)}{n\left(\Omega\right)}\)
\(=1-\dfrac{C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}}{4^{50}}\)
\(\approx0,99295\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 6 2021
Vậy hãy sử dụng 1 phương pháp giải khác tối ưu hơn:
\(\Leftrightarrow2sin^22x=1\)
\(\Leftrightarrow1-2sin^22x=0\)
\(\Leftrightarrow cos4x=0\)
\(\Leftrightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
Với cách giải này thì nghiệm được gộp luôn
CM
21 tháng 1 2018
Đáp án A
Xác suất để Anh được điểm bằng xác suất Anh trả lời đúng câu trong câu còn lại bằng
CM
13 tháng 11 2019
Chọn A
Vì mỗi câu có 4 phương án trả lời và chỉ có một phương án đúng nên xác suất để chọn đúng đáp án là 1 4 , xác suất để trả lời sai là 3 4
Gọi là biến cố bạn Nam được trên 8,5 điểm thì A ¯ là biến cố bạn Nam được dưới 8,5 điểm
Vì bạn Nam đã làm chắc chắn đúng 40c âu nên để có A ¯ xảy ra 2 trường hợp
TH1: Bạn Nam chọn được một câu đúng trong 10 câu còn lại, xác suất xảy ra là:
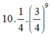
TH2: Bạn Nam chọn được hai câu đúng trong 10 câu còn lại, xác suất xảy ra là:
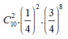
Vậy 
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 10 2021
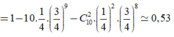
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
\(0< \dfrac{k\pi}{2}< 2017\pi\Rightarrow0< k< 4034\)
Có \(4033\) nghiệm (tất cả các đáp án đều sai)
CM
5 tháng 2 2018
Đáp án A.
Phương pháp: Tính xác suất để học sinh đúng thêm 3 câu nữa trở lên.
Xác suất mỗi câu trả lời đúng là 0,25 và mỗi câu trả lời sai là 0,75.
Cách giải:
An trả lời chắc chắn đúng 45 câu nên có chắc chắn 9 điểm.
Để điểm thi ≥ 9,5 => An phải trả lời đúng từ 3 câu trở lên nữa.
Xác suất để trả lời đúng 1 câu hỏi là 0,25 và trả lời sai là 0,75
TH1: Đúng 3 câu. P1 = 0,253.0,752
TH2: Đúng 49 câu P2 = 0,254.0,75
TH3: Đúng cả 50 câu P3 = 0,254
Vậy xác suất để An được trên 9,5 điểm là P = P1 + P2 + P3 = 13/1024.
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2021
1.
\(\Leftrightarrow1-2sin^2x+sinx+m=0\)
\(\Leftrightarrow2sin^2x-sinx-1=m\)
Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)
Xét hàm \(f\left(t\right)=2t^2-t-1\) trên \(\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{4}\in\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)
\(f\left(-\dfrac{1}{2}\right)=0\) ; \(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\) ; \(f\left(\dfrac{\sqrt{2}}{2}\right)=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow-\dfrac{9}{8}\le f\left(t\right)\le0\Rightarrow-\dfrac{9}{8}\le m\le0\)
Có 2 giá trị nguyên của m (nếu đáp án là 3 thì đáp án sai)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2021
2.
ĐKXĐ: \(sin2x\ne1\Rightarrow x\ne\dfrac{\pi}{4}\) (chỉ quan tâm trong khoảng xét)
Pt tương đương:
\(\left(tan^2x+cot^2x+2\right)-\left(tanx+cotx\right)-4=0\)
\(\Leftrightarrow\left(tanx+cotx\right)^2+\left(tanx+cotx\right)-4=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx+cotx=\dfrac{1+\sqrt{17}}{2}\\tanx+cotx=\dfrac{1-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)
Nghiệm xấu quá, kiểm tra lại đề chỗ \(-tanx+...-cotx\) có thể 1 trong 2 cái đằng trước phải là dấu "+"
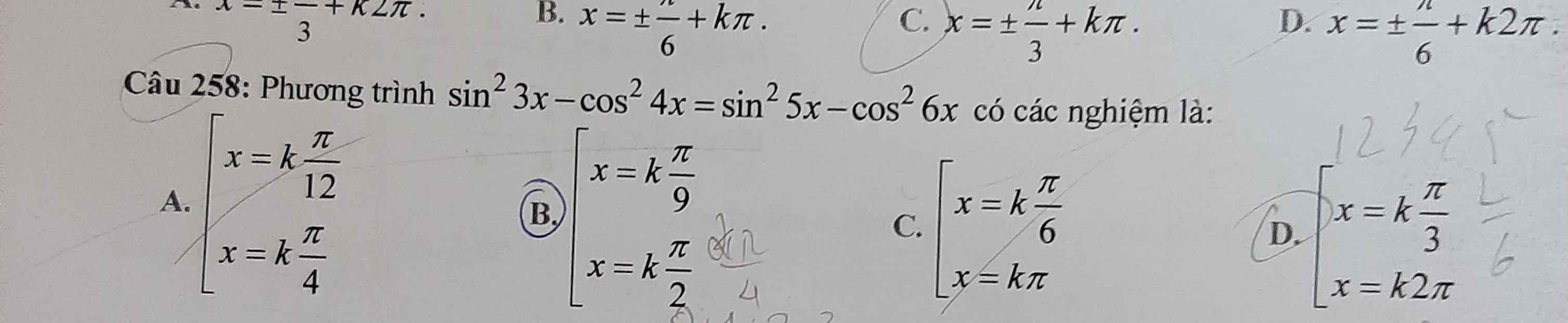
\(-cos6x-cos8x=-cos10x-cos12x\)
\(\Leftrightarrow cos8x-cos12x+cos6x-cos10x=0\)
\(\Leftrightarrow2sin10x.sin2x+2sin8x.2x=0\)
\(\Leftrightarrow sin2x\left(sin10x+sin8x\right)=0\)
\(\Leftrightarrow2sin9x.cosx.sin2x=0\)
\(\Rightarrow\left[{}\begin{matrix}sin9x=0\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{9}\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
P/s: có thể loại ngay các đáp án A, C, D do:
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{12}\\x=\dfrac{k\pi}{4}\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{k\pi}{12}\) (nghiệm \(\dfrac{k\pi}{4}\) là con của họ nghiệm \(\dfrac{k\pi}{12}\) khi thay \(k=3n\) vào \(\dfrac{k\pi}{12}\) ta sẽ được \(\dfrac{k\pi}{4}\))
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{6}\\x=k\pi\end{matrix}\right.\) \(\Rightarrow x=\dfrac{k\pi}{6}\) tương tự như trên
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{3}\\x=k2\pi\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{k\pi}{3}\)