K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
mọi ng hộ e câu 6 vs câu 9 vs ạ
2
5 tháng 6 2021
5)Áp dụng BĐT bunhia ta có:
`P^2<=(1+1+1)(x+y+y+z+z+x)`
`<=>P^2<=3.2(x+y+z)=6`
Mà `P>=0`
`=>P<=sqrt6`
Dấu "=" `<=>x=y=z=1/3`
5 tháng 6 2021
1c của bạn đấy @@
`1c)P=A.B`
`=(sqrtx-1)/(sqrtx+3)*(sqrtx+3)/(sqrtx-3)`
`=(sqrtx-1)/(sqrtx-3)`
`|P|+P=0`
`<=>|P|=-P`
`<=>P<=0`
`<=>(sqrtx-1)/(sqrtx-3)<=0`
Vì `sqrtx-1>sqrtx-3`
`=>` $\begin{cases}\sqrt{x}-1 \ge 0\\\sqrt{x}-3 <0\end{cases}$
`<=>` $\begin{cases}\sqrt{x} \ge 1\\\sqrt{x}<3\end{cases}$
`<=>` $\begin{cases}x \ge 1\\x<9\end{cases}$
`<=>1<=x<9`
Vậy `1<=x<9` thì....
14 tháng 6 2023
b: PTHĐGĐ là;
ax^2=2
=>ax^2-2=0
Δ=0^2-4*a*(-2)=8a
Để (P) cắt (d) tại hai điểm pb thì 8a>0
=>a>0
=>x=căn 2/a hoặc x=-căn 2/a
=>vecto OA=(căn 2/a;0); vecto OB=(-căn 2/a;0); vecto AB=(2*căn 2/a;2)
Theo đề, ta có: vecto OA*vecto OB=0 hoặc vecto OA*vecto AB=0 hoặc vecto OB*vecto AB=0
=>-2*căn 2/a+2=0 hoặc 2*căn 2/a+2=0
=>căn 2/a=1
=>a=2
25 tháng 5 2022
b: Vì (d)//y=-2x+5/2 nên a=-2
Vậy: y=-2x+b
Phương trình hoành độ giao điểm là:
\(0.5x^2+2x-b=0\)
\(\Delta=2^2-4\cdot0.5\cdot\left(-b\right)=4+2b\)
Để (d) tiếp xúc với (P) thì 2b+4=0
hay b=-2
MH
25 tháng 5 2022
Gọi số kg vật liệu xưởng phải sản xuất mỗi ngày theo kế hoạch là \(x\left(kg\right)\left(0< x< 216\right)\)
Thời gian dự định sản xuất là \(\dfrac{216}{x}\) (ngày)
Ba ngày đầu tiên khối lượng vật liệu sản xuất được là \(3x\left(kg\right)\)
Số vật liệu còn lại là \(232-3x\)
Thời gian sản xuất số vật liệu còn lại là \(\dfrac{232-3x}{x+8}\)
Ta có phương trình:
\(\dfrac{216}{x}=3+\dfrac{232-3x}{x+8}+1\)
\(\Rightarrow216\left(x+8\right)=4x\left(x+8\right)+\left(232-3x\right)x\)
\(\Rightarrow216x+1728=4x^2+32x+232x-3x^2\)
\(\Rightarrow x^2+48x-1728=0\Rightarrow\left[{}\begin{matrix}x=24\left(TM\right)\\x=-72\left(L\right)\end{matrix}\right.\)
Vậy theo kế hoạch mỗi ngày xưởng phải sản xuất 24 kg vật liệu.
VD
25 tháng 5 2022
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
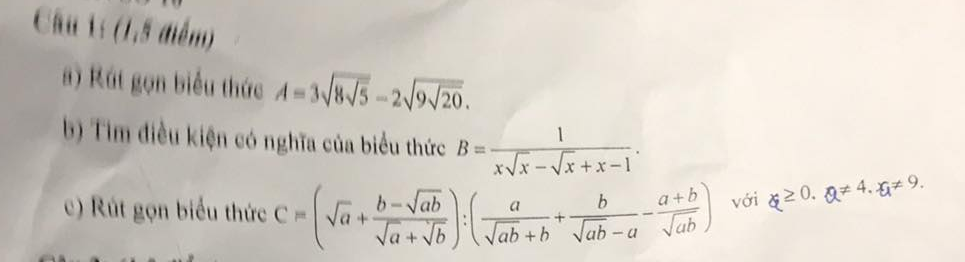
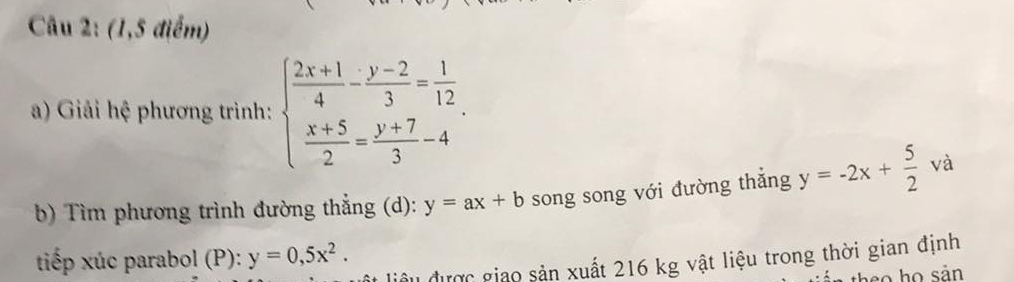
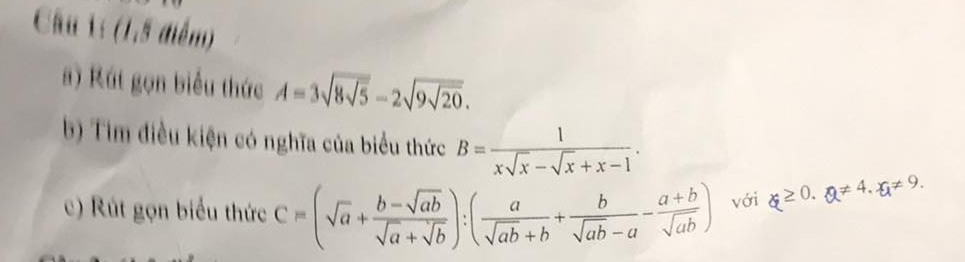
c: \(C=\dfrac{a+\sqrt{ab}+b-\sqrt{ab}}{\sqrt{a}+\sqrt{b}}:\left(\dfrac{a}{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}-\dfrac{b}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{a+b}{\sqrt{ab}}\right)\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}:\dfrac{a\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-b\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)-\left(a+b\right)\left(a-b\right)}{\sqrt{ab}\left(a-b\right)}\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}:\dfrac{a^2-a\sqrt{ab}-b\sqrt{ab}-b^2-a^2+b^2}{\sqrt{ab}\left(a-b\right)}\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}\cdot\dfrac{\sqrt{ab}\left(a-b\right)}{-\sqrt{ab}\left(a+b\right)}\)
\(=-\left(\sqrt{a}-\sqrt{b}\right)\)