Câu 5 : Hai nguyên tố A và B thuộc hai nhóm liên tiếp và ở hai chu kỳ liên tiếp của bảng tuần hoàn. Tổng số proton của A...

NH

Nguyễn Hiền

12 tháng 12 2021

Bài 9. Hai nguyên tố A và B thuộc cùng một nhóm A, ở hai chu kì liên tiếp nhau trong bảng tuần hoàn, tổng số proton trong 2 nguyên tử A và B là 32. Xác định vị trí của A và B trong bảng tuần hoàn?

#Hóa học lớp 10

1

C

chuche

12 tháng 12 2021

Tham Khảo:

A và B là hai nguyên tố ở cùng một phân nhóm và thuộc hai chu kì liên tiếp trong bảng tuần hoàn nên số thứ tự của chúng hơn kém nhau 8 hoặc 18 đơn vị (đúng bằng số nguyên tố trong một chu kỳ).

a,

Theo bài ra, tổng số proton trong hai hạt nhân nguyên tử của A và B bằng 32 nên $Z_{A} + Z_{B} = 32$ (1).

Trường hợp 1: $Z_{B} - Z_{A} = 8 (2) . (1; 2) = > Z_{A} = 12; Z_{B} = 20 .$

A (Magie; chu kỳ 3, nhóm IIA); B: (Canxi; chu kỳ 4, nhóm IIA).

Trường hợp 2: $Z_{B} - Z_{A} = 18 (3); (1; 3) = > Z_{A} = 7; Z_{B} = 25 .$

A (chu kỳ 2, nhóm VA); B: (chu kỳ 4, nhóm VIIB).

Trường hợp này A, B không cùng nhóm nên không thỏa mãn

Đúng(0)

NA

Nguyễn Anh Tú

20 tháng 11 2021

Hai nguyên tố A và B thuộc cùng một nhóm A và ở hai chu kỳ liên tiếp của bảng tuần hoàn. Tổng số điện tích hạt nhân của A và B là 31. a. Xác định A và B? b. Viết cấu hình electron nguyên tử của A và B?

#Hóa học lớp 10

1

CX

Chanh Xanh

20 tháng 11 2021

Tham khảo

Z_A + Z_B = 32

=> { Z_A - Z_B = 8 =>{ Z_A = 20 -> A là Ca

Z_A + Z_B = 32 Z_B = 12 -> B là Mg

Ca: 1s²2s²2p⁶3s²3p⁶4s²

Mg: 1s²2s²2p⁶3s²

Đúng(0)

NH

Nguyễn Hoàng Nam

25 tháng 11 2017

Hai nguyên tố A và B thuộc hai nhóm liên tiếp của bảng tuần hoàn. Tổng số proton của A và B bằng 19. Có bao nhiêu cặp A và B thỏa mãn điều kiện trên

A. 1

B. 2

C. 3

D. 4

#Hóa học lớp 10

1

NQ

Ngô Quang Sinh

25 tháng 11 2017

Đáp án C

Giả sử

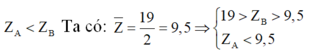
⇒ B thuộc chu kì 3

TH1: A thuộc chu kì 1 (A là Hidro hoặc He)

+ A là Hidro (Z = 1) Không thỏa mãn

+ A là He (Z = 2) Thỏa mãn

TH2: A thuộc chu kì 2 ⇒ A và B là 2 nguyên tố thuộc 2 chu kì nhỏ liên tiếp và 2 nhóm liên tiếp trong bảng tuần hoàn.

Từ đó ta có

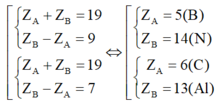(thỏa mãn)

Vậy có 3 trường hợp thỏa mãn điều kiện bài toán.

Đúng(0)

NH

Nguyễn Hoàng Nam

27 tháng 4 2017

Hai nguyên tố A và B thuộc hai nhóm liên tiếp của bảng tuần hoàn. Tổng số proton của A và B bằng 19. Có bao nhiêu cặp A và B thỏa mãn điều kiện trên

A. 1

B. 2

C. 3

D. 4

#Hóa học lớp 10

1

NQ

Ngô Quang Sinh

27 tháng 4 2017

Đáp án C

Giả sử

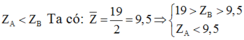
=> B thuộc chu kì 3

TH1: A thuộc chu kì 1 (A là Hidro hoặc He)

+ A là Hidro

Không thỏa mãn

+ A là He (Z = 2)

TH2: A thuộc chu kì 2 => A và B là 2 nguyên tố thuộc 2 chu kì nhỏ liên tiếp và 2 nhóm liên tiếp trong bảng tuần hoàn

Từ đó ta có

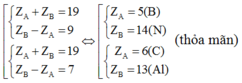
Vậy có 3 trường hợp thỏa mãn điều kiện bài toán.

Đúng(0)

TL

Truong Le Duy

24 tháng 10 2021

Câu 6 : Hai nguyên tố A và B thuộc hai nhóm liên tiếp và ở hai chu kỳ liên tiếp của bảng tuần hoàn. Tổng số hạt mang điện tích trong 2 nguyên tử A và B bằng 50. Hợp chất giữa A và B phải điều chế gián tiếpa. A, B có thể là nguyên tố nào?b. Viết cấu hình e và xác định vị trí trong bảng tuần...

Đọc tiếp

#Hóa học lớp 10

0

NH

Nguyễn Hoàng Nam

7 tháng 10 2017

A và B là hai nguyên tố ở cùng một nhóm và thuộc hai chu kì liên tiếp trong bảng tuần hoàn. Tổng số proton trong hai hạt nhân nguyên tử của A và B bằng 32. Cấu hình electron của A và B lần lượt là A. 1 s 2 2 s 2 2 p 6 3 s 2 và 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 2 B. 1 ...

Đọc tiếp

#Hóa học lớp 10

1

NQ

Ngô Quang Sinh

7 tháng 10 2017

A

A và B là hai nguyên tố ở cùng một phân nhóm và thuộc hai chu kì liên tiếp trong bảng tuần hoàn nên số thứ tự của chúng hơn kém nhau 8 hoặc 18 đơn vị (đúng bằng số nguyên tố trong một chu kỳ).

Theo bài ra, tổng số proton trong hai hạt nhân nguyên tử của A và B bằng 32 nên Z A + Z B = 32 .

● Trường hợp 1: Z B - Z A = 8 . Ta tìm được Z A = 12 ; Z B = 20 .

Cấu hình electron :

A : 1 s 2 2 s 2 2 p 6 3 s 2 (chu kỳ 3, nhóm IIA).

và B: 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 2 (chu kỳ 4, nhóm IIA).

● Trường hợp 2: Z B - Z A = 18 . Ta tìm được Z A = 7 ; Z B = 25 .

Cấu hình electron :

A : 1 s 2 2 s 2 2 p 3 (chu kỳ 2, nhóm VA).

và B: 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 3 d 5 4 s 2 (chu kỳ 4, nhóm VIIB).

Trường hợp này A, B không cùng nhóm nên không thỏa mãn.

Đúng(0)

NN

Nam Nguyễn

10 tháng 11 2021

Câu 5: X và Y thuộc cùng chu kì ở hai nhóm A liên tiếp nhau trong bảng HTTH, tổng số e của X và Y là 51. Xác định X,Y.Câu 8: Hai nguyên tố A và B ở hai nhóm A liên tiếp trong BTH. B thuộc nhóm VA. Ở trạng thái đơn chất A và B không phản ứng với nhau. Tổng số proton trong hạt nhân của A và B là 23. Xác định A, B. Viết cấu hình e và xác định tính chất hóa học cơ bản của chúng.Ai giúp mình 2 câu này với...

Đọc tiếp

#Hóa học lớp 10

0

NP

Nhi Phan

1 tháng 11 2021

Câu : A và B là hai nguyên tố thuộc cùng chu kỳ và cách nhau 1 nhóm trong bảng tuần hoàn. Tổng cố proton của A và B là 28.Xác định số proton của A, và của B.

#Hóa học lớp 10

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP