Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(d_1=90mm\Rightarrow r_1=\dfrac{90}{2}=45mm\)
\(h=156mm\)
\(1oz\) có thể tích là \(29,5ml=29500mm^3\) \(\Rightarrow22oz=295.22=64900mm^3\)
Ta có : \(V_{ly}=\dfrac{1}{3}\pi\left(r_1^2+r_2^2+r_1r_2\right)h\)
\(\Leftrightarrow64900=\dfrac{1}{3}.3,14\left(45^2+r_2^2+45r_2\right)156\)
\(\Leftrightarrow64900=163,28\left(2025+r_2^2+45r_2\right)\)
\(\Leftrightarrow397\approx2025+r_2^2+45r_2\)
\(\Leftrightarrow r_2^2+45r_2-1628=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}r_2\approx24\left(n\right)\\r_2\approx-69\left(l\right)\end{matrix}\right.\)
Đường kính đáy là : \(24.2=48\left(mm\right)\)
\(3500\) ly nằm trong số lượng : Từ \(2000-4999:1065d\)
Vậy 3500 ly thì phải trả số tien là : \(3500.1065=3727500\left(d\right)\)
a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3
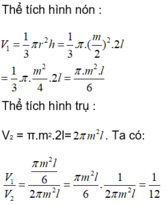
Vậy khi múc đầy nước vào hình nón và đổ vào hình trụ (Không chứa gì cả) thì độ cao của nước trong hình trụ là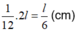 
Vậy chọn đáp án A
a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)
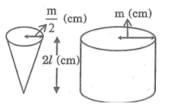
Thể tích của hình trụ là: π m 2 k
Thể tích của hình nón là: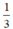 
π
m
2
k
Vậy thể tích của hình nón bằng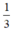 
thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là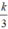 
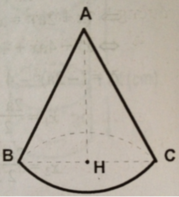
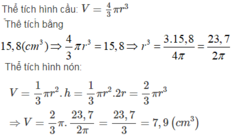
a) Thể tích cái ly:
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.6=8\pi\) \(\left(cm^3\right)\)
b) Thể tích rượu chứa trong ly:
\(V=\dfrac{1}{3}\pi r^2h_r=\dfrac{1}{3}\pi.2^2.3=4\pi\) \(\left(cm^3\right)\)
Sửa lại câu b) nhé em!
Do A'B' // AB và A' là trung điểm của OA
\(\Rightarrow A'B'\) là đường trung bình của \(\Delta OAB\)
\(\Rightarrow A'B'=\dfrac{1}{2}AB=\dfrac{1}{2}.2=1\left(cm\right)\)
Thể tích rượu trong ly:
\(V=\dfrac{1}{3}\pi r^2h_r==\dfrac{1}{3}\pi.1^2.3=\pi\left(cm^3\right)\)