Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIẢI THÍCH:
Gọi công suất mỗi tổ máy là P0.
Ban đầu công suất phát: P1 = 8P0; công suất tiêu thụ là: P 1 ' = 0 , 7 P 1 ;
Hao phí: 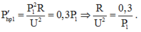 .
.
Công suất tiêu thụ giảm:
![]()
Công suất phát lúc này:

Giải phương trình Ta được: P2/P1 = 2,71 hoặc P2/P1 = 0,63.
Để giảm hao phí thì P2/P1 = 0,63 Þ P2 » 5P0.
Chọn A.

Đáp án B
Gọi số tổ máy ban đầu là n (tổ). Công suất mỗi máy là a (W). Ta có :
- Ban đầu : ![]()
- Sau khi rút 3 tổ máy 
- Sau khi rút x tổ máy để đạt hiệu suất 95% :

Từ (1) và (2) ta có 
Từ (1) và (3) ta có ![]()
Suy ra phải rút tổng cộng 9 tổ máy mới đạt hiệu suất 95% => phải rút thêm 6 tổ máy nữa

Đáp án C
Phương pháp: Sử dụng công thức tính công suất tải, và công suất hao phí
Cách giải: Ta có:
P t = 10 P - ( 10 P ) 2 . R U 2 = 8 P - ( 8 P ) 2 . R ( a U ) 2
Từ (*) và (**), ta có:
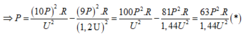
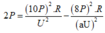
⇒ 2 P = 100 a 2 - 64 P 2 . R a 2 U 2 ( * * )
Từ (*) và (**), ta có:
![]()
⇒ 12 , 5 a 2 = 64 ⇒ a ≈ 2 , 26

Đáp án C
Phương pháp: Sử dụng công thức tính công suất tải, và công suất hao phí
Cách giải:
Ta có: 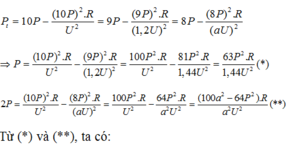
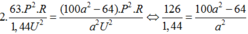
![]()

Chọn đáp án A
+ Khi chưa tăng công suất nơi tiêu thụ ta có: ![]() với
với ![]()
+ Khi tăng công suất nơi tiêu thụ lên 10% ta có:
![]()
![]()
+ Lập tỉ số 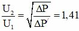

GIẢI THÍCH: P phát không đổi và U hai đầu cuộn sơ cấp không đổi. Khi đó hiệu điện thế hai đầu cuộn thứ cấp là KU
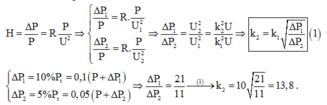
Chọn B.
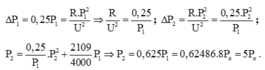
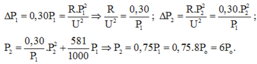
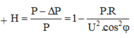
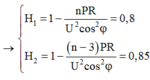
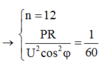
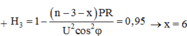
GIẢI THÍCH:
P
U
ΔP
P’
8
U
8 – 6 = 2
75%.8 = 6
x
U
81,25%.6 = 4,875
Chọn A.