Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bỏ qua ma sát hệ là kín theo phương ngang áp dụng định luật bảo toàn động lượng:
\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=\left(m_1+m_2\right)\overrightarrow{v}\left(1\right)\)
Chọn chiều (+) là chiều chuyển động của m1
a) (1) => \(m_1v_1+m_2v_2=\left(m_1+m_2\right)v\Rightarrow v=\dfrac{m_1v_1+m_2v_2}{m_1+m_2}=\dfrac{4}{3}\left(m/s\right)\)
vật sau va chạm chuyển động cùng chiều (+)
b) (1) => \(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\Rightarrow v=\dfrac{m_1v_1-m_2v_2}{m_1+m_2}=\dfrac{2}{3}\left(m/s\right)\)
vật sau va chạm chuyển động cùng chiều (+)

Chọn C.
Ta có: v2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
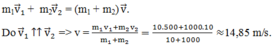

Chọn C.
Ta có: v 2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
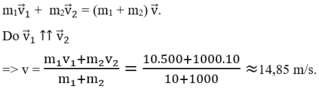

Chọn A.
Độ biến thiên động lượng của vật sau va chạm là:

=> ∆p = mv2 – (–mv1) = m(v2 + v1) = 2 kg.m/s.

a. Ta có: \(v=v_0+at\Leftrightarrow10=0+a5\Leftrightarrow a=2\) (m/s2)
b. Áp dụng định luật II-Niuton có:
\(\overrightarrow{F_{ms}}+\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\)
Chiếu các vector lực lần lượt theo phương Ox, Oy có:
Oy: N=P
Ox: \(-N\mu_t+F=ma\) \(\Leftrightarrow-mg\mu_t+F=ma\Leftrightarrow-2.10.\mu_t+8=2.2\Rightarrow\mu_t=0,2\)
c. (Vẽ lại trục Oxy, sao cho Oy trùng với phương của \(\overrightarrow{N}\), Ox trùng với phương chuyển động)
Áp dụng định luật II-Niuton có:
\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\)
Lần lượt chiếu các vector lực lên phương Ox, Oy có:
Oy: \(N=P.cos30\)
Ox: \(-F_{ms}-P.sin30=ma\)
\(\Leftrightarrow-N\mu_{t'}-mg.sin30=ma\Leftrightarrow-mg.cos30.\mu_{t'}-mg.sin30=ma\)
\(\Leftrightarrow-10.cos30.0,3-10.sin30=a\Leftrightarrow a=-7,6\) (m/s2)

Chọn A.
Độ biến thiên động lượng của vật sau va chạm là:
∆ p ⇀ = m v 2 ⇀ - m v 1 ⇀
Do v 2 ⇀ ↑↓ v 1 ⇀ , chọn chiều dương là chiều của v 1 ⇀ .
=> ∆ p = m v 2 - - m v 1
= m( v 2 + v 1 ) = 2 kg.m/s.

mặc định mảnh nhỏ là m1 còn mảnh to là m2 nhé
a) Áp dụng định lý hàm cos:
\(p_2^2=p_1^2+p^2-2p_1p\cos\left(p_1;p\right)\)
\(\Rightarrow p_2=\sqrt{p_1^2+p^2-2p_1p\cos\left(p_1;p\right)}=....\Rightarrow v_2=\dfrac{p_2}{m_2}\) Thay số vào nốt là xong bạn
\(\cos\left(p_2;p\right)=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}=.....\)
b) Mảnh nhỏ bay lên theo phương thẳng đứng cho ta hình dạng của 1 tam giác vuông
\(p_2=\sqrt{p^2+p_1^2}=\sqrt{\left(mv\right)^2+\left(m_1v_1\right)^2}=...\) \(\Rightarrow v_2=\dfrac{p_2}{m_2}=.....\) (....bạn tự tính điền vào )
\(\cos\left(p_2;p\right)=\dfrac{p}{p_2}=......\) tính nốt :D

Chọn: C.
Chọn địa điểm A làm gốc tọa độ, chọn gốc thời gian lúc hai xe khởi hành, chiều từ A đến B là chiều dương.
Do vậy, vào thời điểm t = 0:
Xe từ A có: x0A = 0; v0A = 36 km/h;
Xe từ B có: x0B = 180 km; v0B = -54 km/h
Suy ra phương trình chuyển động của hai xe lần lượt là:
xA = 36t; xB = 180 – 54t.
Khi hai xe gặp nhau: xA = xB
⟺ 36t = 180 – 54t ⟹ t = 2 h
=> Khi gặp nhau, hai xe có tọa độ: xA = 36.2 = 72 km.

p1 = m1v1 = 1.3 = 3kg.m/s
p2 = m2v2 = 3.1 = 3kg.m/s
a) Động lượng của hệ: =
=  1 +
1 +  2
2
Độ lớn của hệ: p = p1 + p2 = 3 + 3 = 6kg.m/s
b) Động lượng của hệ: =
=  1 +
1 +  2
2
Độ lớn của hệ: p = | p1 - p2 | = | 3 - 3 | = 0kg.m/s
c) Động lượng của hệ: =
=  1 +
1 +  2
2
Độ lớn của hệ: \(p=\sqrt{p^2_1+p_2^2}=\sqrt{3^2+3^2}=4,242kg.m/s\)
d) Động lượng của hệ: =
=  1 +
1 +  2
2
Độ lớn của hệ: p = p1 = p2 = 3kg.m/s