Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y (m) lần lượt là chiều rộng và chiều dài của sân trường.
Điều kiện: 0 < x < 170; 0 < y < 170.
Vì chu vi của sân trường bằng 340 m nên ta có: 2(x + y) = 340
Vì ba lần chiều dài hơn bốn lần chiều rộng là 20m nên ta có: 3y – 4x = 20
Ta có hệ phương trình:
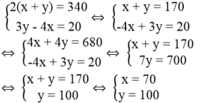
Giá trị của x và y thỏa điều kiện bài toán.
Vậy chiều rộng của sân trường là 70m,
chiều dài của sân trường là 100m.

Gọi chiều rộng sân trường là x (m)(x > 0)
Chiều dài sân trường là y (m) (y > x > 0)
Sân trường có chu vi là 340 m nên ta có : 2(x + y) = 340
Ba lần chiều dài hơn 4 lần chiều rộng là 20 m nên ta có: 3y – 4x = 20
Ta có hệ phương trình sau:
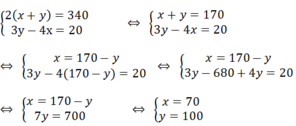
Vậy chiều dài là 100m; chiều rộng là 70m.

Lời giải:
Gọi chiều dài là $a$ và chiều rộng là $b$ (m)
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=340:2=170\\ 3a-4b=20\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=100\\ b=70\end{matrix}\right.\) (m)

Câu trả lời:
Gọi chiều dài và chiều rộng sân trường lần lượt là x và y ( 0<x,y<170 ; x>y)
Vì chu vi là 340 nên ta có PT: x+y=170 (1)
Vì 3 lần chiều dài lớn hơn 4 lầm chiều rộng 20 m nên ta có PT:
3x - 4y = 20 (2)
Từ (1) và (2) ta có HPT :
\(\left\{{}\begin{matrix}x+y=170\\3x-4y=20\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=100\\y=70\end{matrix}\right.\)
Vậy chiều dài là chiều rộng sân trường lần lượt là 100m và 70m.
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của sân trường(Điều kiện: a>0; b>0)
Vì chu vi của sân trường là 340m nên ta có phương trình:
2(a+b)=340
\(\Leftrightarrow a+b=170\)(1)
Vì 3 lần chiều dài hơn 4 lần chiều rộng là 20m nên ta có phương trình:
3a-4b=20(2)
Từ (1) và (2) ta có được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=170\\3a-4b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=510\\3a-4b=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7b=490\\a+b=170\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\a=170-70=100\end{matrix}\right.\)(thỏa ĐK)
Vậy: Chiều dài của sân trường là 100m; Chiều rộng của sân trường là 70m

Nửa chu vi mảnh đất: \(\dfrac{320}{2}=160\left(m\right)\)
Gọi chiều dài mảnh đất là x(m) với x>0
Chiều rộng mảnh đất là: \(160-x\) (m)
Hai lần chiều dài mảnh đất là: \(2x\) (m)
Ba lần chiều rộng là: \(3\left(160-x\right)\) (m)
Do hai lần chiều dài hơn 3 lần chiều rộng là 20m nên ta có pt:
\(2x-3\left(160-x\right)=20\)
\(\Leftrightarrow5x=500\)
\(\Rightarrow x=100\left(m\right)\)
Vậy mảnh đất dài 100m, rộng \(160-100=60\left(m\right)\)

Nửa chu vi hình chữ nhật: 194 : 2 = 97 (m)
Gọi chiều dài là: x (m) (0 < x < 97)
Chiều rộng là: y (m) (0 < x < 97)
Nửa chu vi là 97 nên ta có phương trình:
x + y = 97 (1)
4 lần chiều dài hơn 5 lần chiều rộng là 10m, nên ta có phương trình:
4x - 5y = 10 (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=97\\4x-5y=10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=55\left(TM\right)\\y=42\left(TM\right)\end{matrix}\right.\)
Vậy chiều dài và chiều rộng sân trường lần lượt là: 55m và 42m


Câu 1:
Gọi x là chiều dài mảnh đất (0<x<14; x>y)
Gọi y là chiều rộng mảnh vườn (0<y<14)
Vì chu vi mảnh đất bằng 20m nên ta có PT: x+y=14 (1)
Vì đường chéo mảnh đất bằng 10m nên ta có PT:
x2+y2=100 (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}x+y=14\\x^2+y^2=100\end{matrix}\right.\)(HPT dễ rồi bạn tự giải nha)
⇔\(\left\{{}\begin{matrix}y=8\\y=6\end{matrix}\right.\)(TM)
Vậy ta có 2 tập nghiệm (x;y) là (6;8) và (8;6)
-Độ dài 2 cạnh mảnh đất lần lượt là: 6cm và 8cm
Câu 1:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của mảnh đất(Điều kiện: a>0; b>0 và \(a\ge b\))
Vì chu vi mảnh đất là 28m nên ta có phương trình:
2(a+b)=28
hay a+b=14(1)
Vì đường chéo hình chữ nhật là 10m nên Áp dụng định lí Pytago, ta được:
\(a^2+b^2=100\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=14\\a^2+b^2=100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(14-b\right)^2+b^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-28b+196+b^2-100=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\2b^2-28b+96=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-14b+48=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(b-6\right)\left(b-8\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=14-8=6\\b=14-6=8\end{matrix}\right.\\\left[{}\begin{matrix}b=6\\b=8\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=6\end{matrix}\right.\)(thỏa ĐK)
Vậy: Độ dài hai cạnh của mảnh đất hình chữ nhật lần lượt là 8m và 6m