Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án B
Phương pháp: Áp dụng định luật bảo toàn động lượng, hê ̣thức độc lập với thời gian của vận tốc và li độ ̣
Cách giải:
Ở vị trí cân bằng lò xo dãn một đoạn ∆l.
Ta có k mg 0,05m 5cm
Khi quả cầu đến vị trí thấp nhất thì lò xo đang dãn đoạn: A + ∆l = 12,5 + 5 = 17,5cm và vận tốc của vật bằng 0.
Sau khi va chạm vận tốc hai vật là: mv = (m+M)v’ => 0,5.6 = 1,5.v’ => v’ = 2m/s.
Sau đó hai vật dao động điều hòa, vị trí cân bằng lò xo dãn ∆l’ với : k ' (m M)g ' 0, 075m 7,5cm
Vậy khi x = 10cm, v’ = 2m/s, 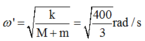
Áp dụng công thức độc lập: 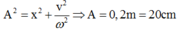

Đáp án D
Va chạm là va chạm mềm nên tại vị trí va chạm: v 0 = m v M + m = v 3 = 2 m / s
Vị trí cân bằng mới của con lắc cách vị trí cân bằng cũ 1 đoạn
OO' = m g k = 0 , 5 . 10 200 = 0 , 025 m = 2 , 5 c m
Ngay sau va chạm con lắc ở vị trí:

Biên độ của con lắc sau va chạm:
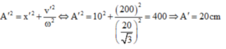

Đáp án C
Khi vật tới biên dưới, vật nhỏ tới va chạm và dính vào nên ta áp dụng bảo toàn động lượng ta có:
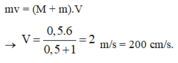
Vị trí cân bằng mới cách vị trí cân bằng cũ 1 đoạn là:
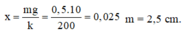
Sau va chạm li độ của vật so với VTCB mới là: x0 = A - x = 10 cm
Biên độ dao động mới của vật là:
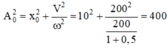
® A0 = 20 cm

Chọn B
+ Vận tốc của hai vật sau va chạm: (M + m)V = mv
![]()
+ Tọa độ ban đầu của hệ hai vật:
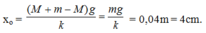
![]()


Hướng dẫn:
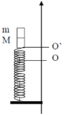
Ta nhận thấy rằng, với cách kích thích dao động bằng va chạm, cho con lắc lò xo nằm thẳng đứng như trên thì cả tần số góc của hệ và vị trí cân bằng của hệ cũng thay đổi.
+ Ban đầu M nằm cân bằng tại O, sau va chạm hệ hai vật sẽ dao động quanh vị trí cân bằng mới O′ nằm dưới O một đoạn Δ l 0 = m g k = 0 , 1.10 25 = 4 cm
+ Tần số góc của hệ hai con lắc sau va chạm ω ' = k M + m = 25 0 , 9 + 0 , 1 = 5
Tại vị trí va chạm hệ hai vật M, m sẽ có li độ x ' = − Δ l 0 = − 4 cm, và có tốc độ tuân theo định luật bảo toàn động lượng v ' = m v 0 m + M = 0 , 1.0 , 2 2 0 , 1 + 0 , 9 = 2 50 m / s
→ Biên độ dao động mới của hệ hai vật A = x ' 2 + v ' ω ' 2 = 4 2 + 2 2 5 2 = 4 cm.
Đáp án D

Giải thích: Đáp án C
Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo kết hợp với định luật bảo toàn động lượng
Cách giải:
+ Theo ĐL bảo toàn động lượng: 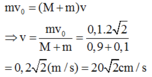
+ Xét con lắc lò xo trước và sau khi va chạm :



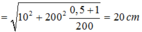
câu 1: Theo bài, sau Δt thì số hạt nhân giảm e lần, tức là \(\frac{No}{N}=e< =>e^{y\text{Δ}t}=e->Y\text{Δ}t=1\)
Tỉ lệ số hạt nhân còn lại so với ban đầu là \(\frac{No}{N}=\frac{N_0e-y\text{Δ}t}{No}=e^{-y\text{Δ}t}=e^{-0,51y\text{Δ}t}=e^{-0,51}=0,6=60\%\)
Bạn lưu ý: Mỗi câu hỏi chỉ hỏi 1 bài toán thôi nhé.
Câu 1: Câu hỏi của trương quang kiet - Học và thi online với HOC24
Câu 2:
Ta có va chạm mềm xảy ra(vì sau va chạm hai vật dính vào nhau).
Theo bảo toàn động lượng:
\(m.v_o =(M+m).v\)
Với v là vận tốc của hệ hai vật sau va chạm.
Tính ra: \(v=40 cm/s\)
Sau va chạm, hệ dao động với tần số góc: \(\omega = \sqrt{\dfrac{k}{M+m}}=10\sqrt 2(rad/s)\)
Ban đầu chỉ có vật M lò xo dãn:
\(\Delta l=\dfrac{Mg}{k}\)
Sau khi có thêm vật m lò xo dãn:\(\Delta l'=\dfrac{(M+m)g}{k}\)
Lượng giãn thêm chính là độ lệch của vật so với vị trí cân bằng cũ, gọi là x
\(x=\Delta l'-\Delta l=\dfrac{m_0g}{k}=0,02m=2cm\)
.\(\Rightarrow A^2=x^2+\left(\dfrac{v}{\omega}\right)^2=2^2+(\dfrac{40}{10\sqrt 2})^2\)
\(\Rightarrow A = 2\sqrt 3cm\)
Tìm động năng cực đại chính là cơ năng của hệ: \(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}.100.(0,02\sqrt3)^2=0,06(J)\)