Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC có chu vi bằng 74cm, AC là cạnh lớn nhất. Đường phân giác của góc A chia cạnh BC thành hai đoạn tỉ lệ với 2:3; đường phân giác của góc C chia cạnh AB thành hai đoạn tỉ lệ với 4:5. Tính độ dài các cạnh của tam giác ABC.
AB + BC + AC = 74 (*)
Trong ∆ ABC phân giác AD → AB/AC = DB/DC = 2/3 (AC > AB)
→ AB = 2/3 . AC (1) , tương tự với phân giác CE ta suy ra
BC = 4/5 . AC (2) . Thế tất cả vào (*) ta được:
2/3 . AC + 4/5 . AC + AC = 74 → 37AC/15 = 74 → AC = 30cm
thế vào (1) và (2) ta được AB = 10cm, BC = 24cm

a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng với ΔMNO
b: A,G,M thẳng hàng và H,G,O thẳng hàng
=>góc AGH=góc MGO
=>ΔAHG đồng dạng với ΔMOG
=>OM/AH=MG/AG
=>OM/AH=MN/AB=1/2
=>GM/GA=1/2
=>G là trọng tâm của ΔACB

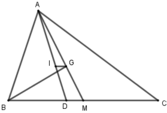
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A

Câu 1: I là giao điểm của 3 đường trung trực nên nó cách đều 3 đỉnh của tam giác đó.
Đáp án: B)
Câu 2: Đáp án: C) 1270
Câu 3: \(AG=\frac{2}{3}AM=\frac{2}{3}.12=8\left(cm\right)\)
Đáp án: A)