Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
b: Xét ΔBMC có BM=BC
nên ΔBMC cân tại B
mà \(\widehat{MBC}=60^0\)
nên ΔBMC đều
c: Xét ΔOBM và ΔOCM có
OB=OC
OM chung
BM=CM
Do đó: ΔOBM=ΔOCM
Suy ra: \(\widehat{OBM}=\widehat{OCM}=90^0\)
hay MC là tiếp tuyến của (O)

a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π

c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.

a: Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
=>ΔMAO=ΔMCO
=>góc MCO=90 độ
góc MAO+góc MCO=180 độ
=>MAOC nội tiếp đường tròn đường kính MO
=>I là trung điểm của MO
b: góc MCO=90 độ
=>MC là tiếp tuyến của (O)
Xét ΔMCD và ΔMBC có
góc MCD=góc MBC
góc CMD chung
=>ΔMCD đồng dạng với ΔMBC
=>MC/MB=MD/MC
=>MC^2=MB*MD
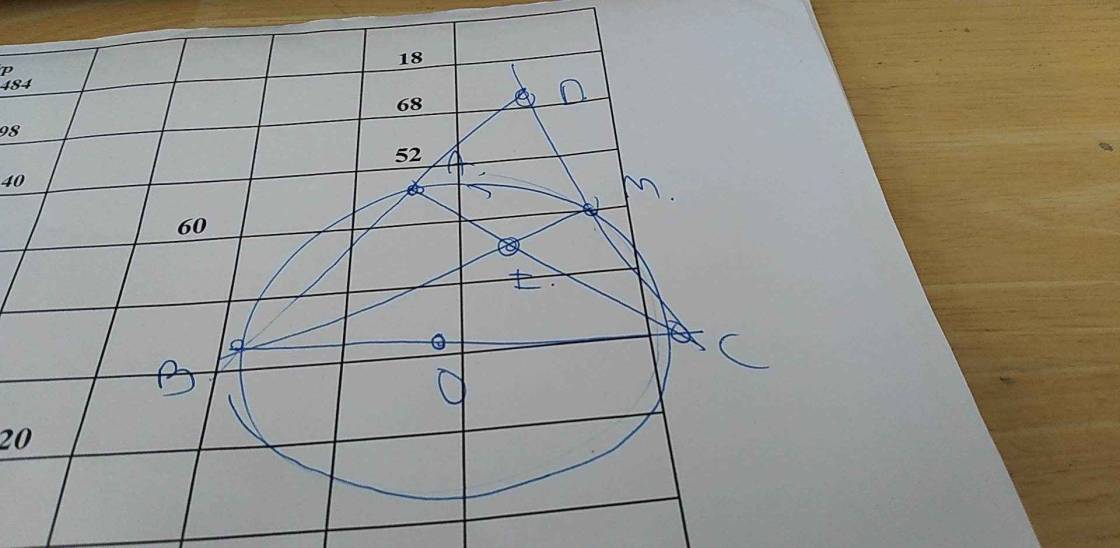
a) Xét (O) có
ΔABC nội tiếp đường tròn(A,B,C∈(O))
AB là đường kính(gt)
Do đó: ΔABC vuông tại C(Định lí)
b) Ta có: \(\widehat{ABC}+\widehat{CBM}=\widehat{ABM}\)(tia BC nằm giữa hai tia BA,BM)
\(\Leftrightarrow\widehat{CBM}+30^0=90^0\)
hay \(\widehat{CBM}=60^0\)
Xét ΔBMC có BM=BC(gt)
nên ΔBMC cân tại B(Định nghĩa tam giác cân)
Xét ΔBMC cân tại B có \(\widehat{CBM}=60^0\)(cmt)
nên ΔBMC đều(Dấu hiệu nhận biết tam giác đều)
c) Xét ΔOBM và ΔOCM có
OB=OC(=R)
OM chung
BM=CM(ΔBMC đều)
Do đó: ΔOBM=ΔOCM(c-c-c)
Suy ra: \(\widehat{OBM}=\widehat{OCM}\)(hai góc tương ứng)
mà \(\widehat{OBM}=90^0\left(gt\right)\)
nên \(\widehat{OCM}=90^0\)
hay OC⊥CM tại C
Xét (O) có
OC⊥CM tại C(cmt)
OC là bán kính(C∈(O))
Do đó: CM là tiếp tuyến của (O)(Dấu hiệu nhận biết tiếp tuyến đường tròn)