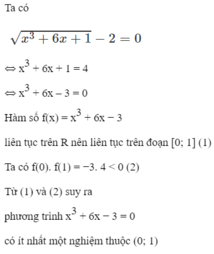Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
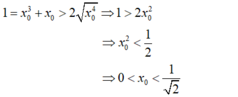

a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx – x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g(π/2) = 1. (-π/2) < 0 nên phương trình đã cho có nghiệm trong khoảng (0; π/2).
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).

a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật