Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
[Phương pháp tự luận]
![]()

Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
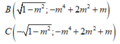
![]()
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
![]()
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)

+ Ta có: y’ = 6x2-6( 2m+1) x+ 6m(m+1)
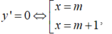
do đó hàm số luôn có cực đại cực tiểu với mọi m.
+ Tọa độ các điểm CĐ, CT của đồ thị là A( m; 2m3+3m2+1 ) và B( m+1; 2m3+3m2)
Suy ra AB = √2 và phương trình đường thẳng AB: x+ y-2m3-3m2-m-1=0.
+ Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
d ( M , A B ) = 3 m 2 + 1 2 ⇒ d ( M , A B ) ≥ 1 2 ⇒ m i n d ( M , A B ) = 1 2
đạt được khi m=0
Chọn B

Chọn B
Ta có:
![]()
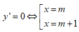
⇒ ∀ m ∈ ℝ , hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
![]()
Suy ra A B = 2
và phương trình đường thẳng x + y - 2 m 3 - 3 m 2 - m - 1 = 0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
Ta có:
![]()
![]()
⇒ đạt được khi m = 0
Câu 1:
Ta có: \(y=x^4-2x^2+2\Rightarrow y'=4x^3-4x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Do đó 3 điểm cực trị của đồ thị hàm số là:
\(A(0;2);B(1;1);C(-1;1)\)
\(\Rightarrow \left\{\begin{matrix} AB=\sqrt{(0-1)^2+(2-1)^2}=\sqrt{2}\\ BC=\sqrt{(1--1)^2+(1-1)^2}=2\\ AC=\sqrt{(0--1)^2+(2-1)^2}=\sqrt{2}\end{matrix}\right.\)
Vì \(AB^2+AC^2=BC^2\) nên tam giác $ABC$ là tam giác vuông tại $A$
\(\Rightarrow S_{ABC}=\frac{AB.AC}{2}=\frac{\sqrt{2}.\sqrt{2}}{2}=1\)
Đáp án A
Câu 2:
Để hàm số đạt cực trị tại $x=1$ thì:
\(y'=-3(m^2+5m)x^2+12mx+6=0\) tại $x=1$
hay \(-3(m^2+5m)+12m+6=0\)
\(\Leftrightarrow m^2+m-2=0\)
\(\Leftrightarrow m=1; m=-2\)
Với m=1:
Hàm số trở thành:
\(y=-6x^3+6x^2+6x-6\)
\(y'=-18x^2+12x+6=0\Leftrightarrow x=1; x=-\frac{1}{3}\)
Lập bảng biến thiên ta thấy thỏa mãn
Với m=-2
Hàm trở thành: \(y=6x^3-12x^2+6x-6\)
\(y'=18x^2-24x+6=0\Leftrightarrow x=1; x=\frac{1}{3}\)
Lập bảng biến thiên ta thấy tại $x=1$ đạt cực tiểu nên không thỏa mãn
Vậy m=1
Đáp án A