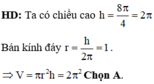Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

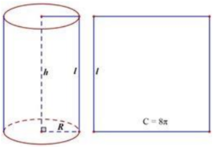
Ta có chu vi hình vuông bằng 8 π ⇒ cạnh hình vuông bằng 2 π
Do đó hình trụ có bán kính R=1, đường sinh l = 2 π (cũng chính là đường cao).
Vậy thể tích hình trụ
V = πR 2 h = 2 π 2
Chọn đáp án A.

Đáp án A
2 π R = 4 R + 2 h ⇒ h = R ( π − 2 ) ⇒ S x q S t p = 2 π R h 2 π R h + 2 π R 2 = π − 2 π − 1

Đáp án C.
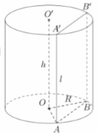
Gọi R,h,l lần lượt là bán kính đáy, chiều cao, đường sinh của hình trụ.
Ta có diện tích xung quanh S x q = 4 π ⇔ 2 πRl = 4 π ⇒ Rl = 2 .
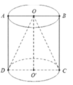
Giả sử AB là một dây cung của đường tròn đáy của hình trụ và căng một cung 120 ° . Vì ABA’A’ là hình chữ nhật có AA' = h = l.
Xét tam giác OAB cân tại O, có O A = O B = R A O B ^ = 120 ° ⇒ A B = R 3 .
Vậy diện tích cần tính là S A B B ' A ' = A B . A A ' = R 3 . 1 = 2 3 .

Chọn C.
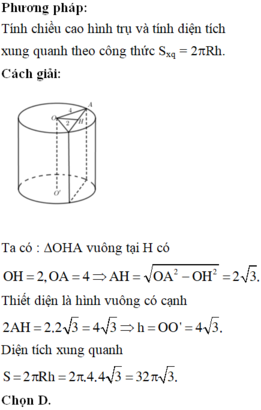
Phương pháp
Công thức tính diện tích xung quanh hình trụ S x q = 2 π R h
Cách giải:
Do thiết diện là hình vuông cạnh a nên bán kính đáy bằng a 2 và chiều cao h = a.
Diện tích xunh quanh: S = 2 π . a 2 . a = π a 2