Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi chiều cao, bán kính đáy của hình trụ lần lượt là h ; r ( h ; r > 0 )
⇒ 2 πr = 2 . ( 2 r + h ) ⇒ h = ( π - 2 ) r
Khi đó:
S x q S t p = 2 πrh 2 πr ( h + r ) = h h + r = π - 2 π - 1

Chọn đáp án D.
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
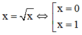
Thể tích cần tính:
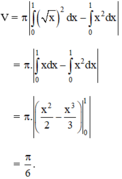

Chọn A.
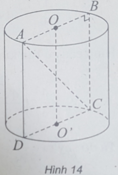
(h.14) Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6 π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = π R 2 h = 72 π ( cm 3 )

Đáp án: D.
Hướng dẫn: Thể tích khối tròn xoay này được tính bởi
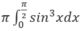

Đáp án C
Do thiết diện là một tam giác đều nên diện tích thiết diện là:
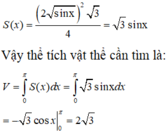

Chọn A.
Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.
Do đó thể tích khối trụ là:
V = πR 2 h = 2 πa 3
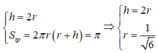
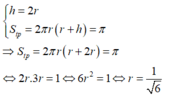
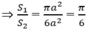
Đáp án D
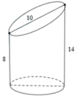
Bán kính đường tròn đáy là:
R = 10 2 - 6 2 2 = 4
Khi đó ta dễ dàng tính được thể tích hình vẽ là:
V = π . 4 2 . 8 + π . 4 2 . 6 2 = 176 π (đvtt).