Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
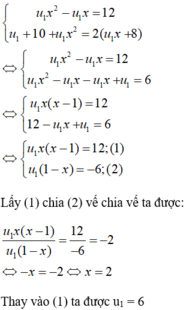
+ Tổng của năm số hạng đầu của CSN là:


Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4

u 12 = 23 S 12 = 144 ⇒ u 1 + 11 d = 23 12 2 u 1 + u 12 = 144 ⇔ u 1 + 11 d = 23 u 1 + 23 = 24 ⇔ u 1 = 1 d = 23 − u 1 11 = 2
Chọn đáp án A
a)
Nhận xét: Tổng của các số hạng ở mỗi cột bằng nhau và bằng 26
b) Tổng các số hạng của cấp số cộng là: 26.8/2 = 104