Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
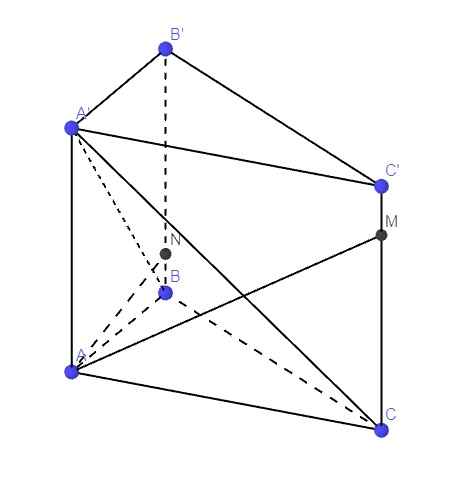
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)

Bài 2:
Ta có: \(y=\frac{x-2}{x-1}\Rightarrow y'=\frac{1}{(x-1)^2}\)
Do đó pt tiếp tuyến của đồ thị (C) tại \(M(a, \frac{a-2}{a-1})\) là:
\(y=f'(a)(x-a)+f(a)\)
\(\Leftrightarrow y=\frac{1}{(a-1)^2}(x-a)+\frac{a-2}{a-1}\) (d)
Đường thẳng trên có vecto pháp tuyến \((\frac{1}{(a-1)^2}, -1)\) nên vecto chỉ phương là: \((1, \frac{1}{(a-1)^2})\)
Vecto chỉ phương của đường thẳng \(\overrightarrow{IM}\) là \((a-1,\frac{a-2}{a-1}-1)\)
Vì hai đường thẳng trên vuông góc với nhau nên:
\(\overrightarrow{d}.\overrightarrow{IM}=\overrightarrow{0}\)
\(\Leftrightarrow (1, \frac{1}{(a-1)^2})(a-1, \frac{a-2}{a-1}-1)=0\)
\(\Leftrightarrow a-1+\frac{1}{(a-1)^2}\left(\frac{a-2}{a-1}-1\right)=0\)
\(\Leftrightarrow a-1-\frac{1}{(a-1)^3}=0\)
\(\Leftrightarrow (a-1)^4=1\Leftrightarrow a=2, a=0\)
\(\Rightarrow \left[\begin{matrix} M=(2, 0)\\ M=(0,2)\end{matrix}\right.\)
Bài 1:
Gọi tọa độ điểm \(M(a,a^3-3a+1)\)
Có: \(y=x^3-3x+1\Rightarrow y'=3x^2-3\). Phương trình tiếp tuyến của (C) tại điểm $M$ là:
\(y=y'(a)(x-a)+y(a)\)
\(\Leftrightarrow y=(3a^2-3)(x-a)+a^3-3a+1\)
Để qua M kẻ được đúng một tiếp tuyến tới $(C)$ thì phương trình hoành độ giao điểm:
\((3a^2-3)(x-a)+a^3-3a+1=x^3-3x+1(*)\) chỉ có đúng duy nhất một nghiệm.
Ta có:
\((*)\Leftrightarrow (x^3-a^3)-(3x-3a)-(x-a)(3a^2-3)=0\)
\(\Leftrightarrow (x-a)(x^2+xa+a^2-3a^2)=0\)
\(\Leftrightarrow (x-a)(x^2+xa-2a^2)=0\)
\(\Leftrightarrow (x-a)^2(x+2a)=0\)
Để pt có nghiệm duy nhất thì \(a=-2a\Leftrightarrow a=0\)
\(\Rightarrow M(0,1)\)