
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




13 . b ) SH \(\perp\left(ABCD\right)\Rightarrow SH\perp DI\) .
Dễ dàng c/m : DI \(\perp HC\) . Suy ra : \(DI\perp\left(SHC\right)\Rightarrow DI\perp SC\) ( đpcm )
Thấy : \(\left(SBC\right)\cap\left(ABCD\right)=BC\)
C/m : SB \(\perp BC\) . Thật vậy : \(BC\perp AB;BC\perp SH\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
Có : \(AB\perp BC\) nên : \(\left(\left(SBC\right);\left(ABCD\right)\right)=\left(SB;AB\right)=\widehat{SBA}=60^o\)

- Mọi số nguyên n đều có số đối của nó là -n
- Do đó, trong biểu thức \(k2\pi\) nếu em thay k bằng số đối của nó là -k thì ta được \(-k2\pi\) thôi

1.
\(sin2x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{6}+k2\pi\\2x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{7\pi}{12}+k\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{7\pi}{12};\dfrac{11\pi}{12}\right\}\)
3.
\(tan\left(2x-15^0\right)=1\)
\(\Rightarrow2x-15^0=45^0+k180^0\)
\(\Rightarrow x=30^0+k90^0\)
\(\Rightarrow x=\left\{-60^0;30^0\right\}\)

2.
\(cos\left(x-5\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow cos\left(x-5\right)=cos\left(\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=\dfrac{\pi}{6}+k2\pi\\x-5=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5+\dfrac{\pi}{6}+k2\pi\\x=5-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{5-\dfrac{11\pi}{6};5-\dfrac{13\pi}{6}\right\}\)
4.
\(\Leftrightarrow cot3x=cot\left(-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x=-\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{9}+\dfrac{k\pi}{3}\)
\(-\dfrac{\pi}{2}< x< 0\Rightarrow-\dfrac{\pi}{2}< -\dfrac{\pi}{9}+\dfrac{k\pi}{3}< 0\)
\(\Rightarrow-\dfrac{7}{6}< k< \dfrac{1}{3}\)
\(\Rightarrow k=\left\{-1;0\right\}\)
\(\Rightarrow x=\left\{-\dfrac{4\pi}{9};-\dfrac{\pi}{9}\right\}\)

a) \(\left(2m-1\right)sinx+1-m=0\Rightarrow sinx=\dfrac{m-1}{2m-1}\)
Pt có nghiệm: \(-1\le\dfrac{m-1}{2m-1}\le1\)
\(\Rightarrow1-2m\le m-1\le2m-1\Rightarrow m\ge\dfrac{2}{3}\)
b) \(\left(m+1\right)sin3x-cos3x=m+2\)
Pt có nghiệm: \(\left(m+1\right)^2+\left(-1\right)^2\ge\left(m+2\right)^2\)
\(\Rightarrow m^2+2m+1+1\ge m^2+4m+4\)
\(\Rightarrow-2m\ge2\Rightarrow m\le-1\)

3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)






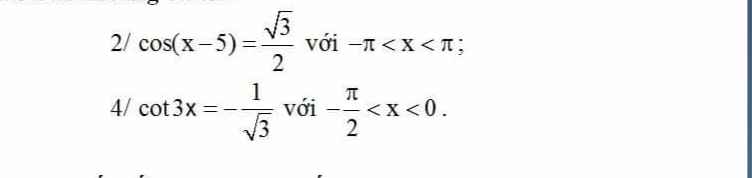


Chúc bạn sang năm mới (tức là lớn thêm một tuổi đó:>) thì bạn sẽ tìm được nhiều niềm vui mới trong cuộc sống bản thân nha!