Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=x^3-\dfrac{6}{5}x^2+\dfrac{12}{25}x-\dfrac{8}{125}\)
b: \(=27m^6+\dfrac{27}{4}m^4n+\dfrac{9}{4}m^2n^2+\dfrac{1}{64}n^3\)

sử dụng tính chất của dãy tỉ số bằng nhau
Vô câu hỏi tương tự mà tham khảo
Tự làm đi nhóc cái này còn cơ bản nên suy nghĩ chút đi
Ta có: \(\frac{x}{10}=\frac{y}{6}=\frac{z}{3}\) => \(\frac{2x}{20}=\frac{3y}{18}=\frac{2z}{6}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{20}=\frac{3y}{18}=\frac{2z}{6}=\frac{2x+3y-2z}{20+18-6}=\frac{16}{32}=\frac{1}{2}\)
=> \(\hept{\begin{cases}\frac{x}{10}=\frac{1}{2}\\\frac{y}{6}=\frac{1}{2}\\\frac{z}{3}=\frac{1}{2}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{1}{2}.10=5\\y=\frac{1}{2}.6=3\\z=\frac{1}{2}.3=\frac{3}{2}\end{cases}}\)
Vậy ...

Hình em tự vẽ nhé.
Từ B ta kẻ BI vuông góc với ME, căt ME tại I. Dễ dàng chứng minh được tam giác BHI bằng tam giác EIH nên BH = EI.
Mà EI = ME+MI. Vậy để chứng minh: MD+ME=BH ta chỉ cần chứng minh MI=MD.
Do BỊ vuông góc EI, EI vuông góc với AC nên BỊ song song AC.
Vậy: \(\widehat{IBC}=\widehat{ACB}\)(hai góc so le trong).
DO tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}.\)Suy ra: \(\widehat{IBC}=\widehat{ABC}.\)
Xét tam giác BMD và tam giác BMI:
Có BM chung .
\(\widehat{IBC}=\widehat{ABC}.\)
\(\widehat{D}=\widehat{I}=90^o.\)
Vậy: \(\Delta BMD=\Delta BMI\)(ch. gn).
Suy ra: IM=MD. Vậy ta có điều phải chứng minh.

a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).

a: Xét ΔAMC và ΔBMD có
MA=MB
\(\widehat{AMC}=\widehat{BMD}\)
MC=MD
Do đó: ΔAMC=ΔBMD

\(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}=\dfrac{6c-15a+10b-6c}{9+4}=\dfrac{10b-15a}{13}\)
\(\Rightarrow\dfrac{3a-2b}{5}=\dfrac{10b-15a}{13}\Rightarrow39a-26b=50b-75a\)
\(\Rightarrow114a=76b\Rightarrow b=\dfrac{3}{2}a\)
Tương tự:
\(\dfrac{2c-5a}{3}=\dfrac{3a-2b}{5}=\dfrac{5b-3c}{2}=\dfrac{15a-10b}{25}=\dfrac{10b-6c}{4}=\dfrac{15a-10b+10b-6c}{25+4}=\dfrac{15a-6c}{29}\)
\(\Rightarrow\dfrac{2c-5a}{3}=\dfrac{15a-6c}{29}\Rightarrow58c-145a=45a-18c\)
\(\Rightarrow76c=190a\Rightarrow c=\dfrac{5}{2}a\)
Thế vào \(a^2+275=bc\)
\(\Rightarrow a^2+275=\left(\dfrac{3}{2}a\right).\left(\dfrac{5}{2}a\right)=\dfrac{15}{4}a^2\)
\(\Rightarrow\dfrac{11}{4}a^2=275\Rightarrow a^2=100\Rightarrow a=\pm10\)
- Với \(a=10\Rightarrow b=\dfrac{3}{2}a=15\) ; \(c=\dfrac{5}{2}a=25\)
- Với \(a=-10\Rightarrow b=-15;c=-25\)

a, Xét hai tam giác vuông ABH và tam giác vuông ACH có :
góc AHB = góc AHC = 90độ
AB = AC ( vì tam giác ABC cân tại A )
cạnh AH chung
Do đó : tam giác ABH = tam giác ACH ( cạnh huyền - cạnh góc vuông )
=> HB = HC ( cạnh tương ứng )
và góc BAH = góc CAH ( góc tương ứng )
b,Xét tam giác AHE và tam giác AHF có :
góc AEH = góc AFH = 90độ
cạnh AH chung
góc HAE = góc HAF ( theo câu a )
Do đó ; tam giác AHE = tam giác AHF ( cạnh huyền - góc nhọn )
=> AE = AF ( cạnh tương ứng )
=> tam giác AEF cân tại A
=> góc AEF = góc AFE = \(\frac{180^0-\widehat{A}}{2}\) ( 1 )
Vì tam giác ABC là tam giác cân nên :
góc ABC = góc ACB = \(\frac{180^0-\widehat{A}}{2}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : góc AEF = góc AFE = góc ABC = góc ACB
mà góc AEF = góc ABC và ở vị trí đồng vị
=> EF // BC .
Học tốt
 cácbạn giúp mik vs hạn 9h tối nay,mong mọi người rep và giải hộ mik
cácbạn giúp mik vs hạn 9h tối nay,mong mọi người rep và giải hộ mik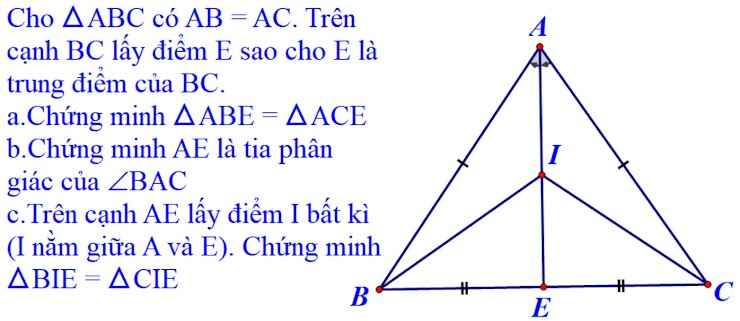


a: \(=27a^3+27a^2+9a+1\)
b: \(=64-96b+48b^2-8b^3\)
c: \(=8c^3+36c^2d+54cd^2+27d^3\)