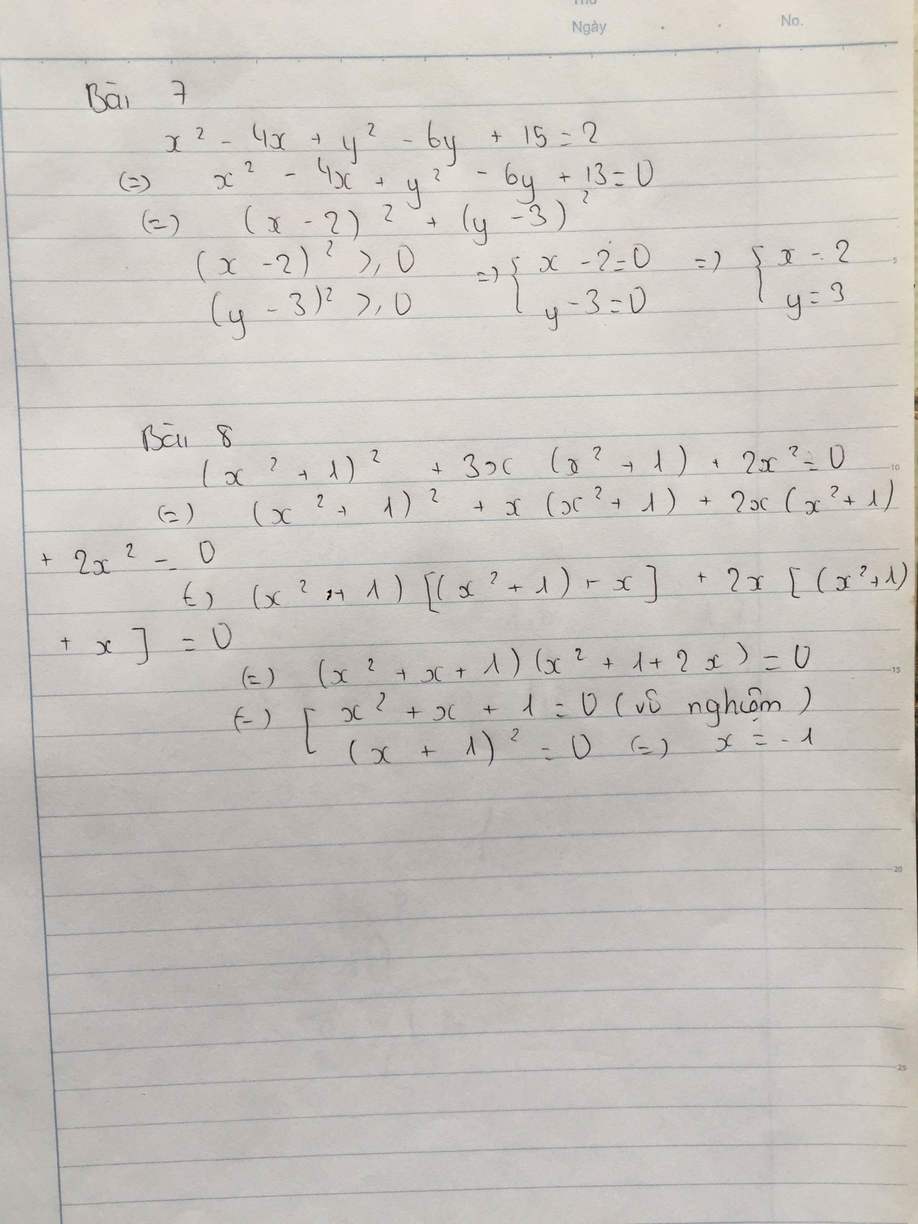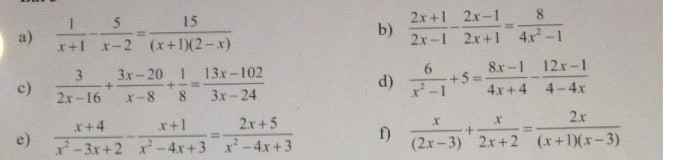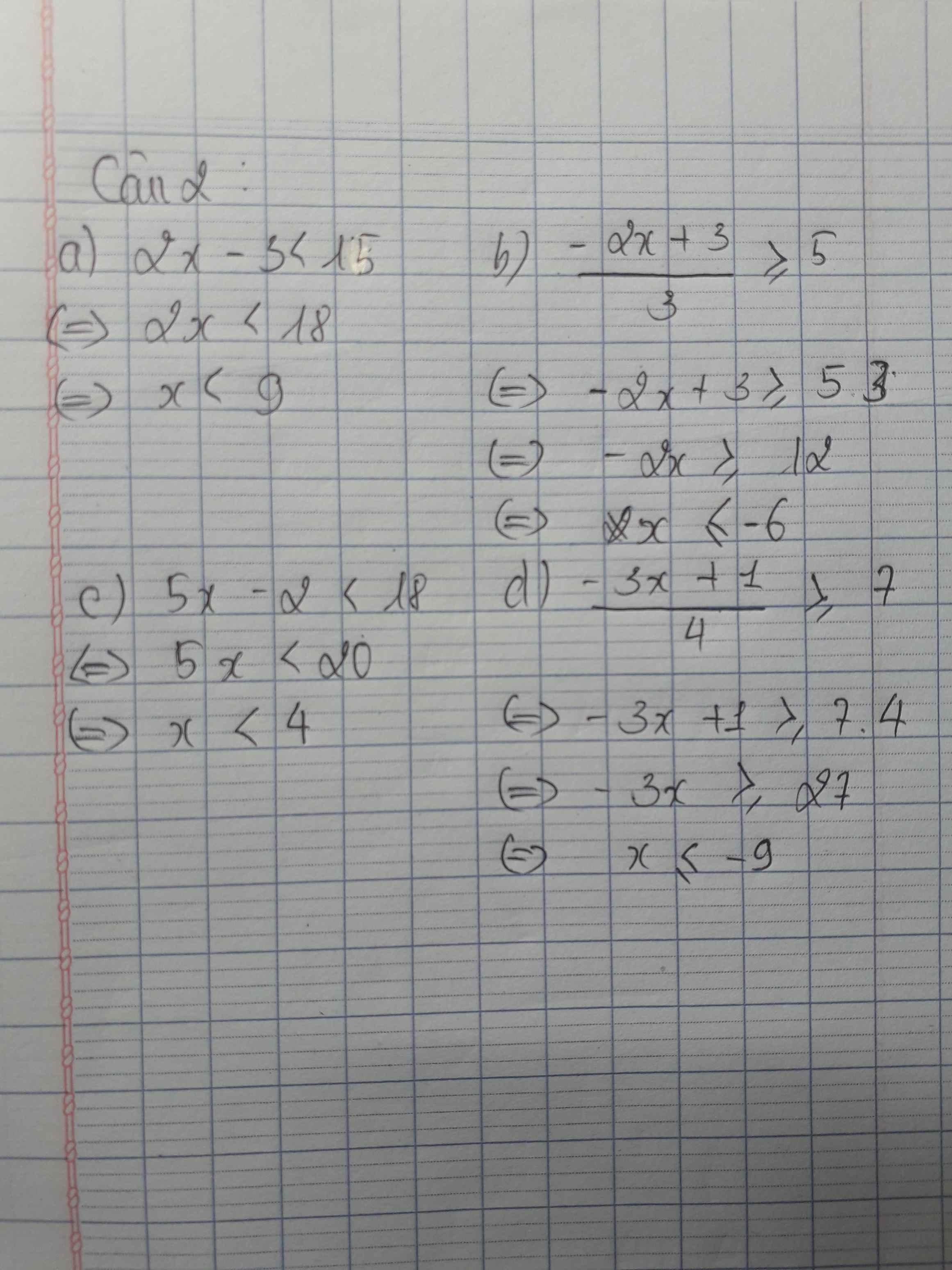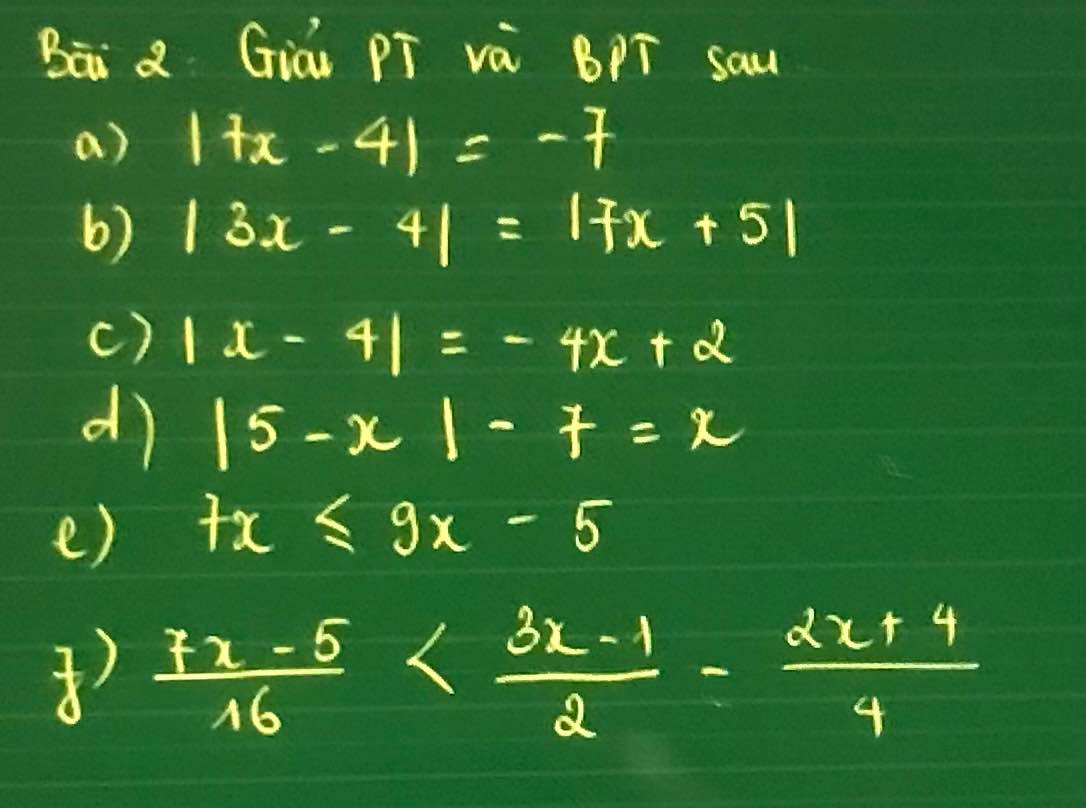K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 2 2022
Bài 6:
\(\dfrac{x-1}{2013}+\dfrac{x-2}{2012}+\dfrac{x-3}{2011}=\dfrac{x-4}{2010}+\dfrac{x-5}{2009}+\dfrac{x-6}{2008}\)
⇔\(\dfrac{x-1}{2013}-1+\dfrac{x-2}{2012}-1+\dfrac{x-3}{2011}-1=\dfrac{x-4}{2010}-1+\dfrac{x-5}{2009}-1+\dfrac{x-6}{2008}-1\)⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}=\dfrac{x-2014}{2010}+\dfrac{x-2014}{2009}+\dfrac{x-2014}{2008}\)
⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}-\dfrac{x-2014}{2010}-\dfrac{x-2014}{2009}-\dfrac{x-2014}{2008}=0\)
⇔\(\left(x-2014\right)\left(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
Vì \(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\ne0\)
\(\Rightarrow x-2014=0\)
⇔\(x=2014\).
-Vậy \(S=\left\{2014\right\}\).
Bài 7:
\(x^2-4x+y^2-6y+15=2\)
⇔\(x^2-4x+y^2-6y+15-2=0\)
⇔\(x^2-4x+y^2-6y+13=0\)
⇔\(\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
⇔\(\left(x-2\right)^2+\left(y-3\right)^2=0\)
Vì \(\left(x-2\right)^2\ge0,\left(y-3\right)^2\ge0\).
\(\Rightarrow\)\(\left(x-2\right)^2=0\) và \(\left(y-3\right)^2=0\)
⇔\(x=2\) và \(y=3\).
Bài 8:
\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)
⇔\(\left(x^2+1\right)^2+2x\left(x^2+1\right)+x^2+x\left(x^2+1\right)+x^2=0\)
⇔\(\left(x^2+1+x\right)^2+x\left(x^2+1+x\right)=0\)
⇔\(\left(x^2+1+x\right)\left(x^2+1+x+x\right)=0\)
⇔\(x^2+x+1=0\) (vô nghiệm, bạn tự c/m) hay \(x^2+2x+1=0\)
⇔\(x^2+2x+1=0\)
⇔\(\left(x+1\right)^2=0\)
⇔\(x=-1\).
-Vậy \(S=\left\{-1\right\}\)
30 tháng 3 2022
a: A=2+7x-5=7x-3
b: x<7/3 nên 3x-7<0
=>B=7-3x+2x+3=10-x
25 tháng 6 2023
c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)
8 tháng 5 2022
Câu 1:
a)2x-3=5
\(\leftrightarrow\)2x=5+3
\(\leftrightarrow\)2x=8
\(\leftrightarrow\)x=4
Vậy pt có tập nghiệm S={4}
b)(2x+1)(x-3)=0
\(\leftrightarrow\) 2x+1=0
Hoặc x-3=0
\(\leftrightarrow\)x=-1/2
x=3
Vậy pt có tập nghiệm S={-1/2;3}
d)3x-4=11
\(\leftrightarrow\)3x=11+4
\(\leftrightarrow\)3x=15
\(\leftrightarrow\)x=5
Vậy pt có tập nghiệm S={5}
e)(2x-3)(x+2)=0
\(\leftrightarrow\)2x-3=0
Hoặc x+2=0
\(\leftrightarrow\)x=3/2
hoặc x=-2
Vậy pt có tập nghiệm S={3/2;-2}
Câu 2:
a)2x-3<15
\(\leftrightarrow\)2x<15+3
\(\leftrightarrow\)2x<18
\(\leftrightarrow\)x<9
Vật bpt có tập nghiệm S={x|x<9}
c)5x-2<18
\(\leftrightarrow\)5x<20
\(\leftrightarrow\)x<4
Vậy bpt có tập nghiệm S={x|x<4}
Mấy bài phân số nhác gõ quá~
PK
0
NT
1
MH
30 tháng 3 2022
a) \(\left|7x-4\right|=-7\)
Mà \(\left|7x-4\right|\ge0\forall x\)
\(\Rightarrow\) phương trình vô nghiệm
b) \(\left|3x-4\right|=\left|7x+5\right|\)
\(\Rightarrow\left[{}\begin{matrix}3x-4=7x+5\\3x-4=-7x-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{9}{4}\\x=-\dfrac{1}{10}\end{matrix}\right.\)
Vậy ...
PK
2
13 tháng 2 2022
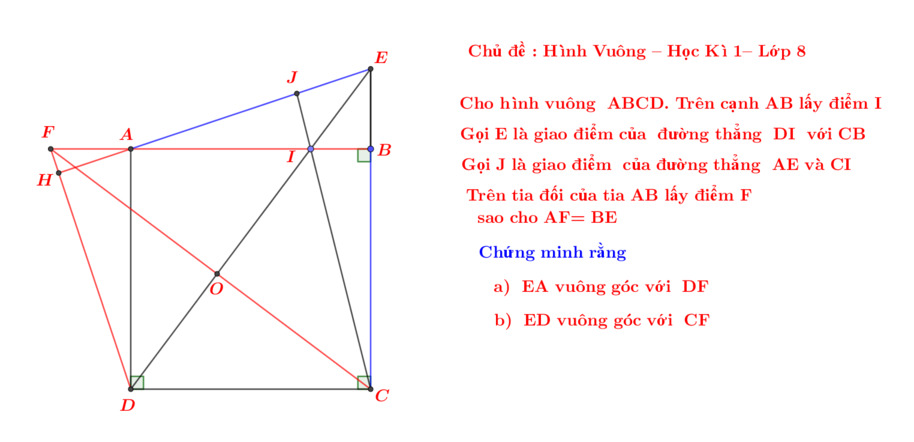
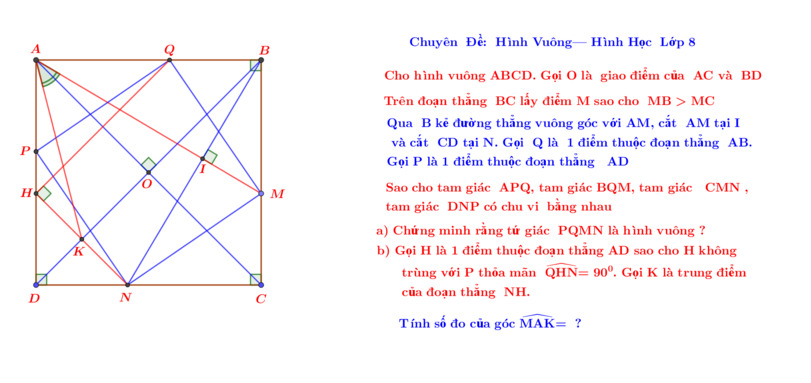
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
