
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a)(-3/5)*x=-1/20+1/2=9/20=>x=9/20:(-3/5)=-3/4\)
Các câu kia làm tương tự nhé, chúc em học giỏi
a: =>-3/5x=-1/20+1/2=-1/20+10/20=-9/20
=>x=3/4
b: =>-1/15x-2/15=3/5
=>-1/15x=6/15+2/15=8/15
=>x=-8
c: \(\Leftrightarrow\left(2x-1\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{\dfrac{1}{2};3;-3\right\}\)

a: \(=\left(6+\dfrac{1}{3}+2+\dfrac{2}{3}\right)+\left(-3-\dfrac{2}{5}-1-\dfrac{3}{5}\right)+4=9-5+4=8\)
b: \(=\dfrac{5}{6}-\dfrac{1}{9}+\dfrac{4}{5}-\dfrac{4}{6}-\dfrac{7}{9}+\dfrac{3}{5}+\dfrac{3}{5}-\dfrac{1}{9}-\dfrac{1}{6}\)
=-1+2=1

Vì AB+BC>AC; AC+BC>AB; AB+AC>BC
nên ba điểm A,B,C không thẳng hàng

Câu 3:
a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
=>OA+AB=OB
hay AB=2(cm)
b: Ta có: A nằm giữa hai điểm O và B
mà OA=AB
nên A là trung điểm của OB
c: Trên đoạn BO, ta có: BC<BO
nên điểm C nằm giữa hai điểm O và B
=>OC+CB=OB
hay OC=3cm
Trên tia Ox, ta có: OA<OC
nên điểm A nằm giữa hai điểm O và C
=>OA+AC=OC
hay AC=1cm

\(d,\dfrac{-25}{12}-\left(\dfrac{23}{12}+1\dfrac{1}{2}\right)=d,\left(\dfrac{-25}{12}-\dfrac{23}{12}\right)-\dfrac{3}{2}=\dfrac{-48}{12}-\dfrac{3}{2}=-4-\dfrac{3}{2}=\dfrac{-8}{2}-\dfrac{3}{2}=-\dfrac{11}{2}\\ e,\dfrac{-1}{9}.\dfrac{-3}{5}-\dfrac{5}{6}.\dfrac{3}{-5}+\dfrac{-5}{2}.\dfrac{3}{5}=\dfrac{1}{9}.\dfrac{3}{5}+\dfrac{5}{6}.\dfrac{3}{5}-\dfrac{5}{2}.\dfrac{3}{5}=\dfrac{3}{5}\left(\dfrac{1}{9}+\dfrac{5}{6}-\dfrac{5}{2}\right)=\dfrac{3}{5}.\dfrac{-14}{9}=\dfrac{-14}{15}\)

Bài 4:
Số thứ hai là 150x3/5=90
Số thứ ba là 90x2/3=60
Số thứ tư là 60x7/10=42
Trung bình của bốn số là:
(150+90+60+42):4=85,5

a: \(\Leftrightarrow2n-2+3⋮n-1\)
\(\Leftrightarrow n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{2;0;4;-2\right\}\)
b \(\Leftrightarrow12n-9⋮3n+1\)
\(\Leftrightarrow12n+4-13⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;13;-13\right\}\)
hay \(n\in\left\{0;-\dfrac{2}{3};4;-\dfrac{14}{3}\right\}\)
c: \(\Leftrightarrow n\left(n-1\right)+1⋮n-1\)
\(\Leftrightarrow n-1\in\left\{1;-1\right\}\)
hay \(n\in\left\{2;0\right\}\)
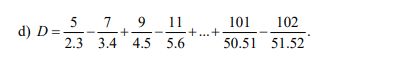
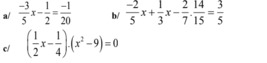
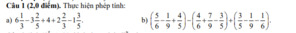
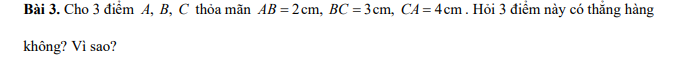


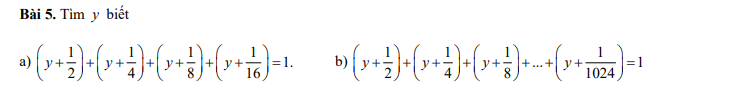
 Các bạn làm nhanh và làm đầy đủ, chính xác nha
Các bạn làm nhanh và làm đầy đủ, chính xác nha 