Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

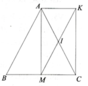
a) Áp dụng tính chất của tam giác cân cho DABC ta có: AM ^ MC và BM = MC
I là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK là hình bình hành
Lại có MK = AC (=2MI)
Þ Tứ giác AMCK là hình chữ nhật.
b) Vì tứ giác AMCK là hình chữ nhật (chứng minh ở a) Þ AK//MC và AK = MC = MB nên tứ giác AKMB là hình bình hành.
c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM= MB.
Þ DMBA cân tại B Þ B A M ^ = A M B ^ = 900 Þ vô lý.
Vậy không có trường hợp nào của D ABC để AKMB là hình thoi.

cau a va b thi minh chac chan roi nhung con cau c thi minh chua chac chan lam:
a) Xet tu giac AMCK co:
I la trung diem cua AC(gt)
KI=MI(k la diem doi xung voi M qua I)
Vay tu giac AMCK la hinh binh hanh(1)
Xet tam giac ABC co
AM la duong trung tuyen
ma tam giac ABC can tai A
vay AM dong thoi la duong cao cua tam giac ABC
hay AM vuong goc voi BC (2)
Tu (1) va (2) suy ra
AKCM la hinh chu nhat
b) AMCK la hinh chu nhat (cm cau a)
Suy ra AK=MC
ma MC=MB(AM duong trung tuyen cua tam giac ABC)
Suy ra AK=MB(3)
ma AK//BM(MC//AK(tinh chat hinh chu nhat))(4)
Tu (3) va (4) suy ra
AKMB la hinh binh hanh
c) De AKMB la hinh thoi khong con truong hop nao nua cua tam giac ABC de thoa man yeu cau hinh binh hanh AKMB la hinh thoi
a) Tứ giác AKMC có AI=CI, MI=IK
=> AKMC là hình bình hành
Mà AMC=90 độ
Vậy AMCK là hình chữ nhật
b) Vì AKMC là hình chữ nhật nên AK//BM
AKMC là hình chữ nhật => AK=MC.
mà MC=BC/2 nên AK=MC/2=BM
Vậy AKMB là hình bình hành

Câu hỏi của Nguyễn Thị Doanh Doanh - Toán lớp 8 - Học toán với OnlineMath
a) ta có IA=IC
IK=IM
=>AMCK là hình bình hành
b) do AKMC là hình bình hành => AK // và =MC=> AK // và =BM( MC và MB cùng nằm tyển BC)
=> AKMB là hình bình hảnh
c) k có

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
a, Vì I là trung điểm MK và AC nên AMCK là hbh
Mà AM là tt nên cx là đường cao
Do đó AM⊥MN nên AMCK là hcn
b, Vì AMCK là hcn nên AK//CM hay AK//MB và AK=CM=BM(do AM là tt)
Do đó AKMB là hbh

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
a, Xét tứ giác AMCK có :
AI=IC (gt)
MI=IK
=> AMCK la HBH
Mà AM là trung tuyến của tam giác ABC
=> AM cũng là đường cao của tam giác ABC
Nên hinh binh hanh AKCM có 1 góc vuông là M=90
=> AKCM là hình chữ nhật
b, Xét tứ giác AKMB co :
AK=MC (tính chất hình chữ nhật AKMC)
Mà BM=MC =>AK=BM (1)
Va AK//MC=>AK//MC (2)
Từ (1)(2) suy ra AKMB là hình bình hành
c, Tam giác ABC phai là tam giác vuông và vuông tại B để tứ giác AKMB là hình thoi