Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Có 
cách chia 20 bạn vào 4 nhóm, mỗi nhóm 5 bạn.
- Gọi A là biến cố “ 5 bạn nữ vào cùng một nhóm”
- Xét 5 bạn nữ thuộc nhóm A có 
cách chia các bạn nam vào các nhóm còn lại.
- Do vai trò các nhóm như nhau nên có 
Khi đó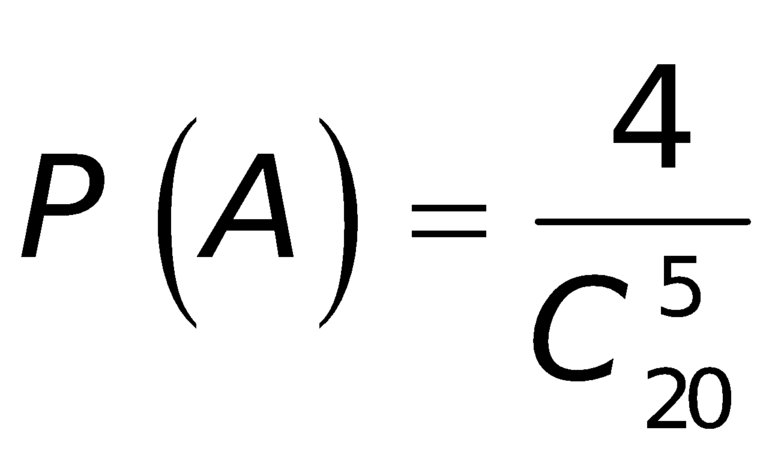 
.
bài này có hai cách làm
cách 1
(1nữ 4nam).(2nữ 3nam)=\((2C1.8C4)+(2C2..8C3)=196\)
cách 2
giả sử không có em nữa nào, ròi láy cái tổng trừ đi
\(10C5-8C5=196\)
Không gian mẫu: \(C_{20}^5.C_{15}^5.C_{10}^5\)
Chọn nhóm cho 5 bạn nữ: có 4 cách
Xếp 15 bạn nam vào 3 nhóm còn lại: \(C_{15}^5.C_{10}^5\)
Xác suất: \(P=\dfrac{4.C_{15}^5.C_{10}^5}{C_{20}^5.C_{15}^5.C_{10}^5}\)
Gọi X là biến cố " chia 20 bạn thành 4 nhóm A, B, C, D mỗi nhóm 5 bạn sao cho 5 bạn nữ thuộc cùng 1 nhóm"
Ta có \(\left|\Omega\right|=C^5_{20}C^5_{10}C^5_5\) cách chia các bạn nam vào 3 nhóm còn lại.
Do vai trò các nhóm như nhau, có \(4C^5_{20}C^5_{10}C^5_5\) cách chia các bạn vào các nhóm A, B, C,D trong đó 5 bạn nữ thuộc một nhóm
Xác suất cần tìm là \(P\left(X\right)=\frac{4}{C^5_{20}}=\frac{1}{3876}\)
Chọn 2 bạn trong số 40 bạn vào đội cờ đỏ nên có C402 cách chọn. Sau khi chọn 2 bạn rồi, chọn 3 trong số 40-2=38 bạn còn lại vào ban chấp hành đoàn nên có C383 cách chọn. Theo quy tắc nhân, có C402. C383 cách chọn
Chọn A
Đáp án D
Mỗi cách chọn là một tổ hợp chập 5 của 15 nên 
Số cách chọn là
Xác suất cần tìm là: 
Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách
ban tổ chúc có số cách chọn
TH1 bạn tốt đc giải nhất
1!x4P1
TH2 bạn Tốt đc giải nhì
1!x4P1
--> só cách chọn là 8 ( cách)
đây là cách nghĩ của mk bạn xe mcos chuẩ nko nhé
Cảm ơn bạn