Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

( giả sử có E nằm trên BC sao cho BD=DE=EC)
S AOB=2 S AOC( vì có chung đấy AO, chiều cao hạ từ B xuống AO gấp 2 lần chiều cao hạ từ C xuống AO)( đoạn so sánh chiều cao, đầu tiên bạn phải chứng minh S ABD=2 S AEC, sau đó, nhận xét, 2 tam giác này có chung cạnh đáy AE, tức là chiều cao hạ từ C xuống AE =1/2 chiều cao hạ từ B xuống AE)
=> S AOB= 18.2=36(cm2)

a) Xét \(\Delta\)AGE đáy GE và \(\Delta\)ADE đáy DE có: \(\frac{GE}{DE}=\frac{1}{2}\)( vì G là trung điểm DE )
=> \(\frac{S\left(AGE\right)}{S\left(ADE\right)}=\frac{1}{2}\)
=> \(S\left(ADE\right)=2.S\left(AGE\right)=2.12=24\left(cm^2\right)\)
Xét \(\Delta\)ADE có đáy AE và \(\Delta\)ADC có đáy CD
mà \(AE=\frac{3}{4}AC\Rightarrow S\left(ADE\right)=\frac{3}{4}S\left(ADC\right)\)
=> \(24=\frac{3}{4}S\left(ADC\right)\)
=> \(S\left(ADC\right)=32\left(cm^2\right)\)
Xét \(\Delta\)ADC có đáy DC và \(\Delta\)ABC có đáy BC
mà \(BD=\frac{1}{5}BC\)=> \(CD=\frac{4}{5}BC\)
=> \(S\left(ABD\right)=\frac{4}{5}S\left(ABC\right)\)
=> \(32=\frac{4}{5}S\left(ABC\right)\)
=> S (ABC) = 5 x 32 : 4 = 40 (cm^2)
b) Tỉ số phần trăm diện tích ADE và ABC là:
24 : 40 x 100= 60 %
Đáp số: 60%

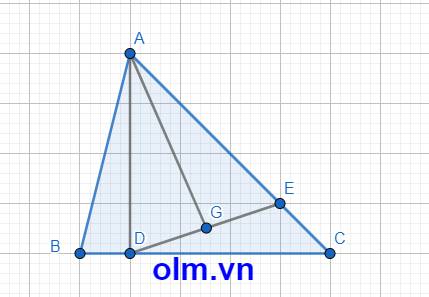
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
Mọi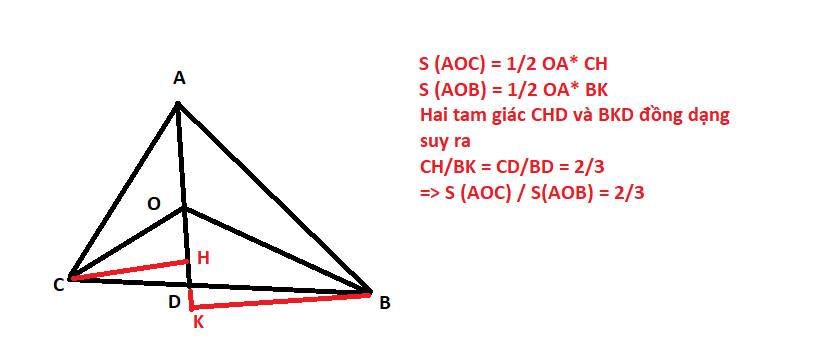
Mọi thắc mắc về Toán có thể liên hệ inbox để có thêm chi tiết