K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TB
0
LD
23 tháng 8 2021
bất đẳng thức cosi là khái niệm dùng để chỉ bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Trong đó, trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng
LD
23 tháng 8 2021
Hệ quả 1: Nếu tổng hai số dương không đổi thì tích của chúng lớn nhất khi hai số đó bằng nhau Hệ quả 2: Nếu tích hai số dương không đổi thì tổng của hai số này nhỏ nhất khi hai số đó bằng nhau
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
Nửa chu vi hình chữ nhật:14 cm
Gọi chiều dài hình chữ nhật là x (cm) với \(7< x< 14\)
Chiều rộng hình chữ nhật là: \(14-x\) (cm)
Diện tích ban đầu của hình chữ nhật: \(x\left(14-x\right)\)
Chiều dài hình chữ nhật sau khi tăng 1cm: \(x+1\)
Chiều rộng sau khi tăng 2cm: \(14-x+2=16-x\)
Diện tích lúc sau: \(\left(x+1\right)\left(16-x\right)\)
Do diện tích tăng lên 25 \(cm^2\) nên ta có pt:
\(\left(x+1\right)\left(16-x\right)-x\left(14-x\right)=25\)
\(\Leftrightarrow x+16=25\)
\(\Leftrightarrow x=9\left(cm\right)\)
Vậy hình chữ nhật ban đầu dài 9cm và rộng 5cm
NT
0
TN
1
16 tháng 11 2021
b: Xét ΔAHC vuông tại H có HM là đường cao
nên \(AM\cdot AC=AH^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=HB\cdot HC\)
TH
1
G
6 tháng 4 2022
Ta có 1ml = 1cm3
Vậy thể tích của lọ đựng dung dịch đó là 100 cm3
Diện tích trong của đáy lọ là:
Ta có: V = S đáy * h => S đáy = V : h = 100 : 12.5 = 8 (cm2)
15 tháng 12 2022
3: \(=7-4\sqrt{3}+7+4\sqrt{3}=14\)
4: \(=\left(\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\right)\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{1}{3}\)
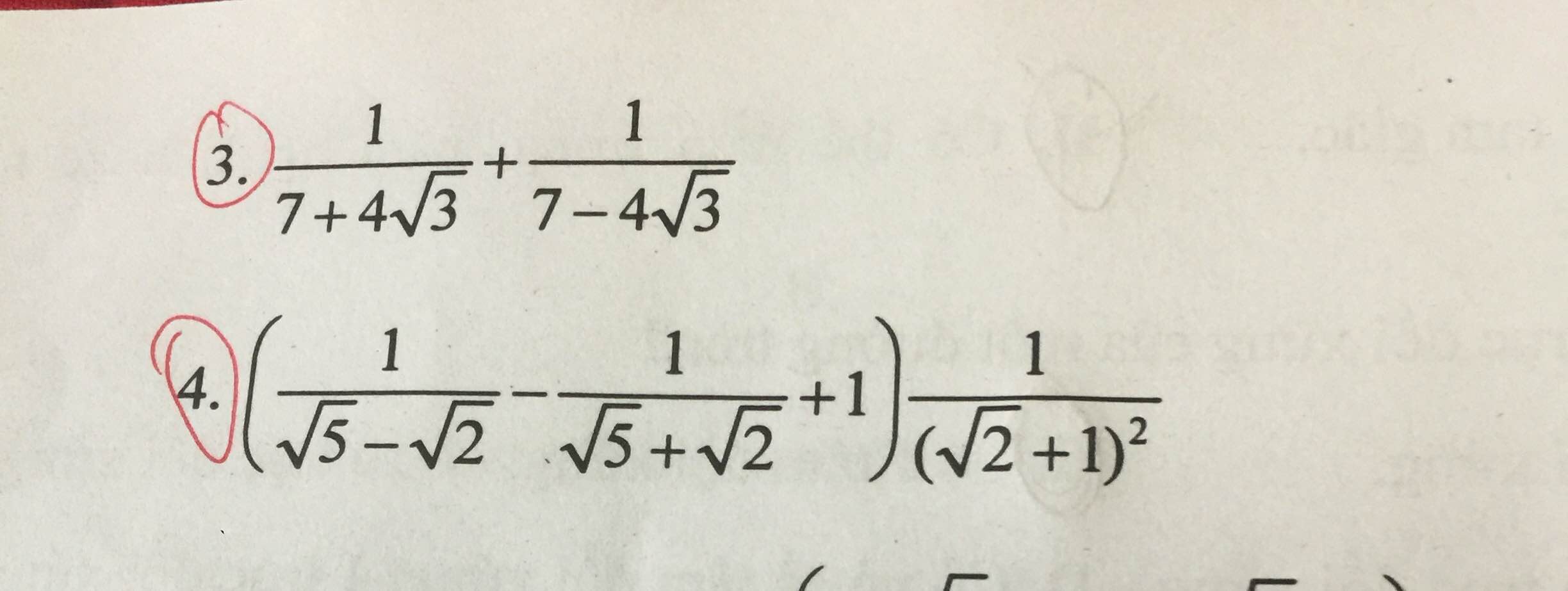
\(a,=\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)\\ b,=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-2\left(\sqrt{x}+\sqrt{y}\right)\\ =\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}-2\right)\\ c,=x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)\)
\(a,=\dfrac{\left(9-4\sqrt{5}\right)\left(5+2\sqrt{5}\right)}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{5-2\sqrt{5}}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{25-10\sqrt{5}+8\sqrt{5}}{20}=\dfrac{25-2\sqrt{5}}{20}\\ b,=\dfrac{\sqrt{x}+2-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\\ c,=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}-\dfrac{2}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}+1-2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}=1\\ d,=\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}+\dfrac{x+1}{1-x}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)