
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(-\dfrac{2}{5}+\dfrac{10}{3}\right):\left(-\dfrac{2}{5}+\dfrac{10}{3}\right)=1\\ e,\Rightarrow\left[{}\begin{matrix}5x-1=0\\2x=\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=\dfrac{1}{6}\end{matrix}\right.\)
2 câu kia đề mờ quá b

12D
Bài 1:
\(a,=\left(\dfrac{11}{19}+\dfrac{8}{19}\right)+\left(\dfrac{19}{18}-\dfrac{1}{18}\right)+5,2=1+1+5,2=7,2\\ c,=\left(\dfrac{5}{12}:\dfrac{10}{3}\right)+\left(\dfrac{1}{6}\right)^2=\dfrac{1}{8}+\dfrac{1}{36}=\dfrac{11}{72}\\ d,=\dfrac{2^4\cdot2^3}{2^6}=2\)
Bài 2:
\(a,\Rightarrow\dfrac{2}{3}x=\dfrac{3}{10}\Rightarrow x=\dfrac{9}{20}\\ b,\Rightarrow x=\dfrac{-2\cdot27}{3,6}=-15\\ c,\Rightarrow\left|x-12\right|=2017\\ \Rightarrow\left[{}\begin{matrix}x-12=2017\\12-x=2017\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2029\\x=-2005\end{matrix}\right.\)

Xét ΔABM và ΔDEN có
AB=DE
\(\widehat{B}=\widehat{E}\)
BM=EN
Do đó: ΔABM=ΔDEN
Suy ra: AM=DN
Ta có:
ΔABC=ΔDEF(gt)ΔABC=ΔDEF(gt)
⇒⎧⎪⎨⎪⎩AB=DEˆABC=ˆABM=ˆDEF=ˆDENBC=EF⇒{AB=DEABC^=ABM^=DEF^=DEN^BC=EF
Ta lại có:
⎧⎪ ⎪⎨⎪ ⎪⎩BM=MC=12BC(gt)EN=NF=12EF(gt){BM=MC=12BC(gt)EN=NF=12EF(gt)
⇒BM=MC=EN=NF⇒BM=MC=EN=NF
Xét ΔABMΔABM và ΔDENΔDEN có:
AB=DE(ΔABC=ΔDEF)AB=DE(ΔABC=ΔDEF)
ˆABM=ˆDEN(cmt)ABM^=DEN^(cmt)
BM=EN(cmt)BM=EN(cmt)
Do đó ΔABM=ΔDEN(c.g.c)ΔABM=ΔDEN(c.g.c)
⇒AM=DN (Hai cạnh tương ứng)
sr bạn mình ko bk vẽ hình trên đây

a) Vì \(\hept{\begin{cases}\left|5-4x\right|\ge0\\\left|7y-3\right|\ge0\end{cases}}\)nên dấu "=" xảy ra <=> x = 5/4 ; y = 3/7
b) Vì \(\hept{\begin{cases}\left|x-3y-1\right|\ge0\\\left|y-4\right|\ge0\end{cases}}\)nên dấu "=" xảy ra <=> x = 13 ; y = 4
a)do |5-4x|+|7y-3|=0,mà|5-4x| và|7y-3| đều lớn hơn hoặc = 0
suy ra 5-4x=7y-3=0 thì biểu thức mới thỏa mãn
(do mọi số trong dấu GTTĐ đều lớn hơn hoặc bằng 0)
tự giải nốt nhé


Bài 5:
a: Bậc của M là 5
b: Các hạng tử là \(x^3yz;-x^5;3\)
Bài 6:
\(N=x^2y-5x^2y-4x^3+7x^2+3xy^2-\dfrac{3}{4}=-4x^2y-4x^3+7x^2+3xy^2-\dfrac{3}{4}\)

5: \(=\dfrac{1}{2}\cdot10-\dfrac{1}{2}=\dfrac{1}{2}\cdot9=\dfrac{9}{2}\)

a: \(\widehat{B}=\dfrac{180^0-80^0}{2}=50^0\)
b: Chiều dài là \(\sqrt{15^2-9^2}=12\left(dm\right)\)

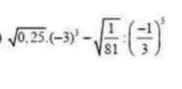 các bạn giúp mik vs , mik đang gấp
các bạn giúp mik vs , mik đang gấp 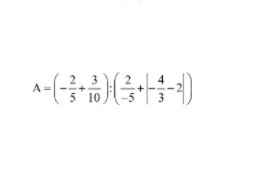
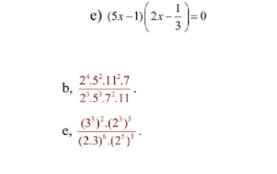 các bạn giúp mik vs mik đang gấp
các bạn giúp mik vs mik đang gấp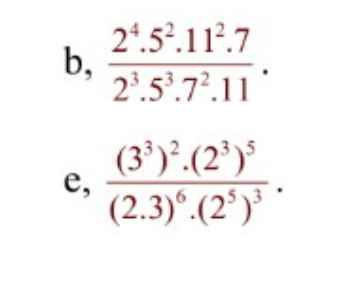 giúp em vs ah
giúp em vs ah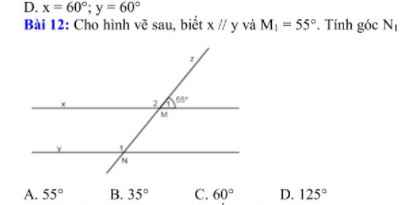
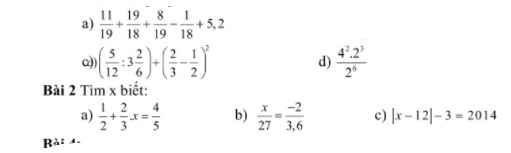 các bạn giúp mik vs mik đang gấp lắm
các bạn giúp mik vs mik đang gấp lắm  giải hộ em bài này vs ạ
giải hộ em bài này vs ạ
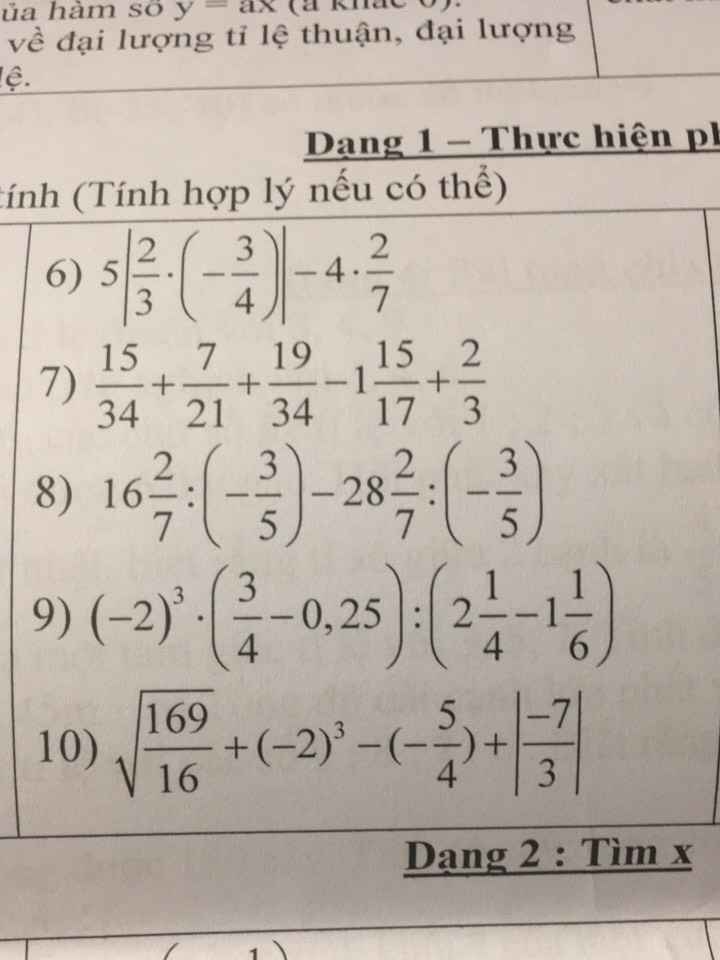
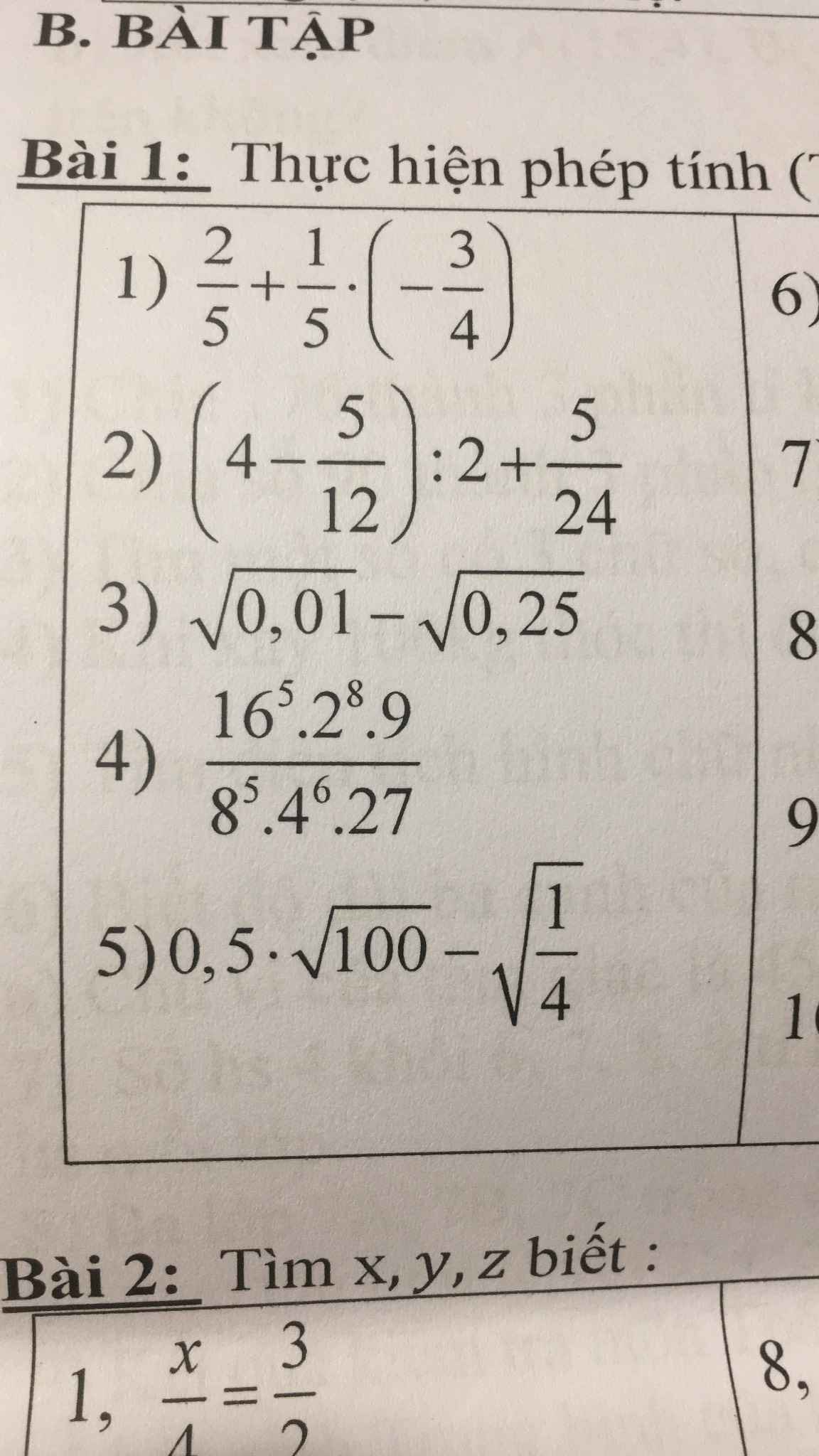


\(=0,5\cdot27-\dfrac{1}{9}:\left(-\dfrac{1}{27}\right)=\dfrac{1}{2}\cdot27+\dfrac{1}{9}\cdot27=27\left(\dfrac{1}{2}+\dfrac{1}{9}\right)=27\cdot\dfrac{11}{18}=\dfrac{33}{2}\)