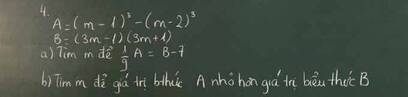các bạn giúp mik với ak
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
26 tháng 12 2021
a) 2x2y(x2+xy-3y2)
= 2x4y + 2x3y2 - 6x2y3
b) (2x+1)(x-1)
= 2x2 - 2x + x -1
= 2x2 -x -1
c) (3xy2+6x2y-9xy):3xy
= y + 2x - 3
d) \(\dfrac{2x+7}{x+1}+\dfrac{x-4}{x+1}\)
= \(\dfrac{2x+7+x-4}{x+1}\)
= \(\dfrac{3x+3}{x+1}\)
= \(\dfrac{3\left(x+1\right)}{x+1}\)= 3
e) \(\dfrac{\left(x+2\right)^2}{x-1}:\dfrac{x+2}{3x-3}\)
= \(\dfrac{\left(x+2\right)^2}{x-1}.\dfrac{3\left(x-1\right)}{x+2}\)
= 3(x+2) = 3x+6
f) \(\left(\dfrac{x^2+2x+2}{x+2}-\dfrac{1}{x+2}\right):\dfrac{x-1}{x+2}\)
= \(\left(\dfrac{x^2+2x+2-1}{x+2}\right):\dfrac{x-1}{x+2}\)
= \(\dfrac{x^2+2x+1}{x+2}.\dfrac{x+2}{x-1}\)
= \(\dfrac{\left(x+1\right)^2}{x-1}\)
4 tháng 10 2021
Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
4 tháng 1 2022
a: Xét tứ giác AKBD có
I là trung điểm của AB
I là trung điểm của DK
Do đó: AKBD là hình bình hành
mà \(\widehat{ADB}=90^0\)
nên AKBD là hình chữ nhật
b: Xét tứ giác AKDC có
AK//DC
AK=DC
Do đó: AKDC là hình bình hành
Suy ra: KD//AC; KD=AC
12 tháng 12 2021
Bài 2:
a: Xét tứ giác CPBM có
N là trung điểm của CB
N là trung điểm của PM
Do đó: CPBM là hình bình hành
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2022
\(\Leftrightarrow18x^2\left(x+4\right)-12x\left(x+4\right)=0\)
\(\Leftrightarrow6x\left(x+4\right)\left[3x-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\\x=\dfrac{2}{3}\end{matrix}\right.\)
MK
1
YN
20 tháng 6 2022
\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)
31 tháng 12 2021
a: Xét tứ giác BHCI có
M là trung điểm của BC
M là trung điểm của HI
Do đó: BHCI là hình bình hành
Suy ra: CI=BH
10 tháng 11 2021
\(\Leftrightarrow\left(5x+1\right)\left(x-4\right)-\left(x-4\right)=0\\ \Leftrightarrow5x\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
