Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, có 2 quả đỏ, 1quả xanh, và 1 vàng : 9C2 x 5C2 x 4C2 =2160cách
b, ta có nếu chọn 6 quả ko cần thứ tự trừ đi cho ko có quả đỏ nào: 18C6 - 14C6=15561 cách
mình viết theo cách bấm trên máy tính mong bạn thông cảm.
Số cách chọn có đúng 2 quả đỏ:
\(C_4^2.C_{14}^4=6006\) cách
Câu b thì bạn kia làm đúng rồi

b. số cách chọn 2 quả cầu màu đỏ và một quả cầu màu xanh là C42.C51= 30
Chọn A

Chọn 4 quả chỉ có màu xanh: \(C_7^4\) cách
Chọn 4 quả chỉ có màu đỏ: \(C_6^4\) cách
Chọn 4 quả chỉ có màu vàng: \(C_5^4\) cách
\(\Rightarrow\) Chọn 4 quả chỉ có màu xanh và đỏ: \(C_{13}^4-\left(C_7^4+C_6^4\right)=665\) cách
Chọn 4 quả chỉ có màu xanh và vàng: \(C_{12}^4-\left(C_7^4+C_5^4\right)=455\) cách
Chọn 4 quả chỉ có màu đỏ và vàng: \(C_{11}^4-\left(C_6^4+C_5^4\right)=310\) cách
Tổng cộng: \(665+455+310=...\)

Đáp án C.
Số cách lấy ngẫu nhiên 4 quả là: C 10 4 (cách)
Số cách lấy được 2 quả đỏ, 2 trắng là: C 4 2 . C 7 2 (cách)
Xác suất để lấy được đúng 2 quả đỏ là:
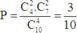

c. Số cách chọn 3 quả cầu trong đó có ít nhất một quả cầu đỏ là:
C41.C52+C42.C51+C43=74
Chọn D

Số cách lấy ra `5` quả bất kì là: `C_10 ^5=252` cách
Số cách lấy ra `5` quả nhưng trong đó không có quả cầu xanh: `C_6 ^5=6` cách
`=>` Số cách lấy ra `5` quả bất kì trong đó có ít nhất `1` cầu xanh là: `252-6=246` cách
(Tối đa có `252` cách lấy mà bạn lại tính ra `504` là điều vô lí, với bài này dùng đối của yêu cầu đề bài sẽ thích hợp nhất)

Lời giải:
YCĐB tương đương với việc lấy ngẫu nhiên 2 cầu từ hộp 1 và 1 cầu từ hộp 2 đều trắng.
Xác suất lấy 2 cầu trắng từ hộp 1 là: $\frac{C^2_{10}}{C^2_{15}}=\frac{3}{7}$
Xác suất lấy 1 cầu trắng từ hộp 2 là: $\frac{C^1_7}{C^1_{15}}=\frac{7}{15}$
Xác suất lấy ngẫu nhiên 2 cầu từ hộp 1 và 1 cầu từ hộp 2 đều trắng là: $\frac{3}{7}.\frac{7}{15}=\frac{1}{5}$

Số cách chọn là: \(C_{5}^{2} . C_{4}^{3}=40\) (cách).
Cảm ơn bạn