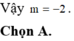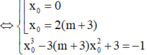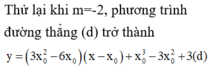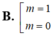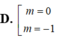Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
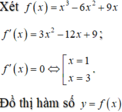

Đồ thị hàm số y = f ( x ) gồm hai phần:
Phần 1. Giữ nguyên phần đồ thị nằm phía trên trục hoành.
Phần 2. Lấy đối xứng phần nằm dưới trục hoành qua trục hoành

Dựa vào đồ thị, ta thấy đường thẳng d và đồ thị (C) có hai điểm chung khi


Chọn A
Ta có ![]() và
và 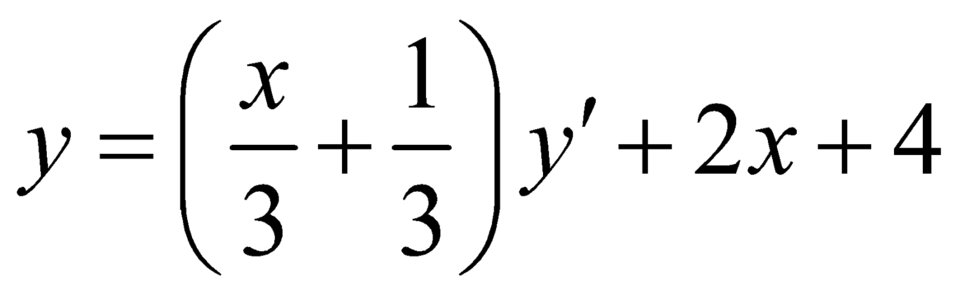 ,
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là ![]() ,
, ![]() .
.
Đường tròn ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]() .
.
Đường thẳng ![]() tiếp xúc với đường tròn
tiếp xúc với đường tròn ![]() khi và chỉ khi
khi và chỉ khi ![]()
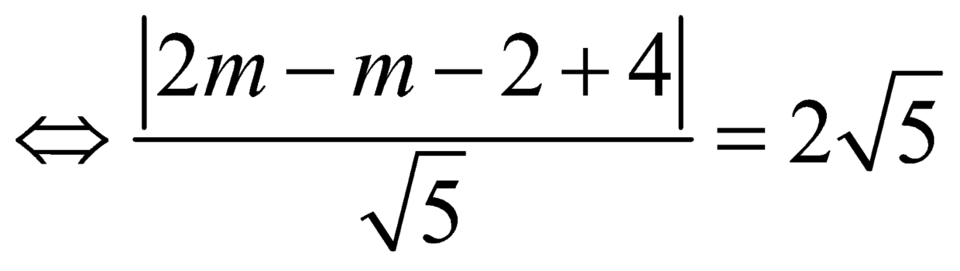
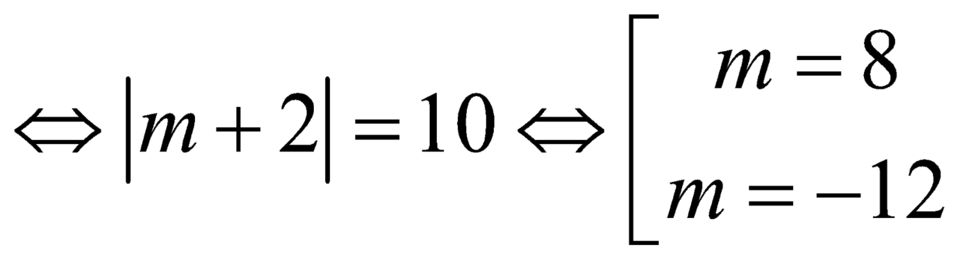 .
.
Vậy ![]() .
.

+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x= 2 có dạng:
∆: y= k( x-2) hay y= kx-2k
+ ∆ là tiếp tuyến của (C)
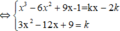
có nghiệm

+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x=2có dạng y= a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B.

Chọn đáp án D.
![]()
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]
Quan sát đồ thị thấy phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ] khi - 1 ≤ m < 1